题目内容
10.已知一次函数y=kx+b的图象经过三点A(0,-2)、B(3,1)、C(m,-4),试求k、b、m的值.分析 首先把A(0,-2)、B(3,1)代入y=kx+b,可得关于k、b的方程组,解方程组可得k、b的值,进而可得一次函数解析式,然后再把C点坐标代入函数解析式可得M的值.
解答 解:∵一次函数y=kx+b的图象经过点A(0,-2)、B(3,1),
∴$\left\{\begin{array}{l}{-2=b}\\{1=3k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-2}\end{array}\right.$,
∴一次函数解析式为y=x-2,
∵图象过C(m,-4),
∴-4=m-2,
解得:m=-2.
点评 此题主要考查了一次函数图象上点的坐标特点,关键是掌握凡是函数图象经过的点,必能满足解析式.

练习册系列答案
相关题目
19.对有序数对(x,y)的一次操作变换记为P1(x,y),定义其变换法则如下:P1(x,y)=(x+y,x-y);且规定Pn(x,y)=P1(Pn-1(x,y))(n为大于1的整数).如P1(1,2)=(3,-1),P2(1,2)=P1(P1(1,2))=P1(3,-1)=(2,4),P3(1,2)=P1(P2(1,2))=P1(2,4)=(6,-2).则P2016(1,-1)=( )
| A. | (0,21007) | B. | ( 21007,-21007) | C. | ( 21008,-21008) | D. | ( 0,21008) |
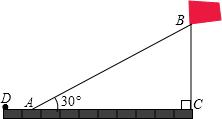 如图,小明利用升旗用的绳子测量学校旗杆BC的高度,当绳子从旗杆端垂下,地上部分还有8米,若把绳子往外拉直,绳子末端接触地面A点并与地面形成30°角,求旗杆BC的高度.
如图,小明利用升旗用的绳子测量学校旗杆BC的高度,当绳子从旗杆端垂下,地上部分还有8米,若把绳子往外拉直,绳子末端接触地面A点并与地面形成30°角,求旗杆BC的高度.