题目内容
20.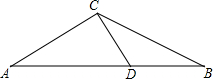 △ABC中,AC=BC,在边AB上截取AD=AC,连接CD,若点D恰好是线段AB的一个黄金分割点,则∠A的度数是( )
△ABC中,AC=BC,在边AB上截取AD=AC,连接CD,若点D恰好是线段AB的一个黄金分割点,则∠A的度数是( )| A. | 22.5° | B. | 30° | C. | 36° | D. | 45° |
分析 根据黄金分割的定义得到AD2=BD•AB,而AD=AC=BC,则BC2=BD•AB,根据相似三角形的判定得△BCD∽△BAC,则∠A=∠BCD,设∠A=x,则∠B=x,∠BCD=x,根据三角形外角性质得∠ADC=∠BCD+∠B=2x,所以∠ACD=∠ADC=2x,然后根据三角形内角和定理得到x+2x+x+x=180°,再解方程即可.
解答 解:∵点D是线段AB的一个黄金分割点,
∴AD2=BD•AB,
∵AD=AC=BC,
∴BC2=BD•AB,
即BC:BD=AB:BC,
而∠ABC=∠CBD,
∴△BCD∽△BAC,
∴∠A=∠BCD,
设∠A=x,则∠B=x,∠BCD=x,
∴∠ADC=∠BCD+∠B=2x,
而AC=AD,
∴∠ACD=∠ADC=2x,
∴x+2x+x+x=180°,解得x=36°,
即∠A=36°.
故选:C.
点评 本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.其中AC=$\frac{\sqrt{5}-1}{2}$AB≈0.618AB,并且线段AB的黄金分割点有两个.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.下列各题的计算,正确的是( )
| A. | (a2)2=a4 | B. | (-3a2)2=-9a4 | C. | (-a)•(-a)4=a5 | D. | a2+a2=2a4 |
5.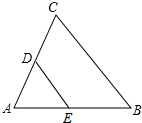 如图,在△ABC中,D、E分别是边AC、AB上的点,下列命题中,假命题是( )
如图,在△ABC中,D、E分别是边AC、AB上的点,下列命题中,假命题是( )
 如图,在△ABC中,D、E分别是边AC、AB上的点,下列命题中,假命题是( )
如图,在△ABC中,D、E分别是边AC、AB上的点,下列命题中,假命题是( )| A. | 若$\frac{AD}{AC}$=$\frac{DE}{BC}$,则△ADE与△ABC相似 | B. | 若$\frac{AD}{DC}$=$\frac{AE}{EB}$,则△ADE与△ABC相似 | ||
| C. | 若$\frac{AD}{AB}$=$\frac{AE}{AC}$,则△ADE与△ABC相似 | D. | 若∠ADE=∠B,则△ADE与△ABC相似 |
12.2014年湖州市许多企业自主创新步伐的加快,专利保护意识的不断增强,我市企业的专利申请量和授权量也不断提高,2014年上半年专利示范企业工业总产值达386.61亿元,用科学记数法表示386.61亿元应该为( )
| A. | 386.61×108 | B. | 0.38661×1011 | C. | 3.8661×1010 | D. | 38.661×109 |