题目内容
1.计算:(1)$\sqrt{18}$-$\frac{2}{\sqrt{2}}$+|1-$\sqrt{2}$|
(2)$\sqrt{48}$÷$\sqrt{3}$+$\sqrt{\frac{1}{2}}$×$\sqrt{12}$-$\sqrt{24}$
(3)($\sqrt{3}$-2$\sqrt{12}$-$\sqrt{6}$)×2$\sqrt{3}$+5$\sqrt{2}$
(4)$\frac{2}{3}$$\sqrt{20}$×(-$\frac{1}{3}$$\sqrt{48}$)÷$\sqrt{2\frac{2}{3}}$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先进行二次根式的乘除运算,然后化简后合并即可;
(3)先进行二次根式的乘法运算,然后化简后合并即可;
(4)根据二次根式的乘除法则运算.
解答 解:(1)原式=3$\sqrt{2}$-$\sqrt{2}$+$\sqrt{2}$-1
=3$\sqrt{2}$-1;
(2)原式=$\sqrt{48÷3}$+$\sqrt{\frac{1}{2}×12}$-2$\sqrt{6}$
=4+$\sqrt{6}$-2$\sqrt{6}$
=4-$\sqrt{6}$;
(3)原式=$\sqrt{3}$×2$\sqrt{3}$-2$\sqrt{12}$×2$\sqrt{3}$-$\sqrt{6}$×2$\sqrt{3}$+5$\sqrt{2}$
=6-24-6$\sqrt{2}$+5$\sqrt{2}$
=-18-$\sqrt{2}$;
(4)原式=$\frac{2}{3}$×(-$\frac{1}{3}$)×$\sqrt{20×48×\frac{3}{8}}$
=-$\frac{4\sqrt{10}}{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
11.股民小明上周末买进某公司股票1000股,每股23元,如表为本周内每日该股票的涨跌情况(单位:元)
(1)星期三收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低价是每股多少元?
(3)已知小明买进股票时付了0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税,如果小明在周末收盘前将全部股票卖出,他的收益情况如何?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +2 | +4.5 | -1 | -2.5 | -2 |
(2)本周内最高价是每股多少元?最低价是每股多少元?
(3)已知小明买进股票时付了0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税,如果小明在周末收盘前将全部股票卖出,他的收益情况如何?
12.下列说法:(1)全等三角形的对应边相等;(2)全等三角形的对应角相等;(3)全等三角形的周长相等;(4)周长相等的两个三角形相等;(5)全等三角形的面积相等;(6)面积相等的两个三角形全等.其中不正确的是( )
| A. | (4)(5) | B. | (4)(6) | C. | (3)(6) | D. | (3)(4)(5)(6) |
6.我国的陆地面积为9600000平方千米,9600000用科学记数法可表示为( )
| A. | 96×105 | B. | 9.6×106 | C. | 0.96×107 | D. | 960×104 |
13.新开通的万家丽快速桥全长约16500米,将16500用科学记数法表示为( )
| A. | 16.5×103 | B. | 1.65×104 | C. | 1.65×103 | D. | 0.165×104 |
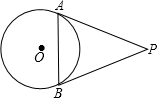 如图,PA、PB分别是⊙O的切线,切点为A、B两点.若∠P=60°,PA=4cm,则AB的长为4cm.
如图,PA、PB分别是⊙O的切线,切点为A、B两点.若∠P=60°,PA=4cm,则AB的长为4cm.