题目内容
16.化简与求值(1)已知A=2m2+n2+2m,B=m2-n2-m,求A-3B;
(2)先化简,再求值:2x2+(2xy-3y2)-2(yx+$\frac{3}{2}{x}^{2}$-2y2),其中(x+1)2+|y-2|=0.
分析 (1)把A与B代入A-3B中,去括号合并即可得到结果;
(2)原式去括号合并得到最简结果,利用非负数的性质求出x与y的值,代入计算即可求出值.
解答 解:(1)∵A=2m2+n2+2m,B=m2-n2-m,
∴A-3B=2m2+n2+2m-3(m2-n2-m)=2m2+n2+2m-3m2+3n2+3m=-m2+4n2+5m;
(2)∵(x+1)2+|y-2|=0,
∴x=-1,y=2,
则原式=2x2+2xy-3y2-2xy-3x2+4y2=-x2+y2=-1+4=3.
点评 此题考查了整式的加减-化简求值,非负数的性质,以及整式的加减,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
7.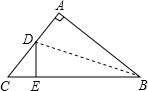 如图,在Rt△ABC中,∠A=90°,AC=6cm,AB=8cm,把AB边翻折,使AB边落在BC边上,点A落在点E处,折痕为BD,则tan∠DBE的值为( )
如图,在Rt△ABC中,∠A=90°,AC=6cm,AB=8cm,把AB边翻折,使AB边落在BC边上,点A落在点E处,折痕为BD,则tan∠DBE的值为( )
 如图,在Rt△ABC中,∠A=90°,AC=6cm,AB=8cm,把AB边翻折,使AB边落在BC边上,点A落在点E处,折痕为BD,则tan∠DBE的值为( )
如图,在Rt△ABC中,∠A=90°,AC=6cm,AB=8cm,把AB边翻折,使AB边落在BC边上,点A落在点E处,折痕为BD,则tan∠DBE的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{3}{10}$ | C. | $\frac{3\sqrt{73}}{73}$ | D. | $\frac{\sqrt{10}}{10}$ |
8.如果x是最大的负整数,y是绝对值最小的整数,则-x2015+y的值是( )
| A. | 2015 | B. | -1 | C. | 1 | D. | -2015 |
5.已知点A(m-1,3)与点B(2,n-1)关于x轴对称,则(m+n)2015的值为( )
| A. | 0 | B. | -1 | C. | 1 | D. | 32015 |
6.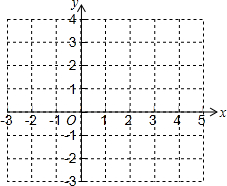 对于抛物线y=x2-4x+3.
对于抛物线y=x2-4x+3.
(1)它与x轴交点的坐标为(1,0),(3,0),与y轴交点的坐标为(0,3);
(2)在坐标系中利用描点法画出此抛物线:
(3)根据图象说明:当x为何值时,函数y随着x的增大而增大?当x为何值时,函数y随着x的增大而减小?
 对于抛物线y=x2-4x+3.
对于抛物线y=x2-4x+3.(1)它与x轴交点的坐标为(1,0),(3,0),与y轴交点的坐标为(0,3);
(2)在坐标系中利用描点法画出此抛物线:
| x | … | … | |||||
| y | … | … |
 如图,是长清园博园内的一个矩形花园,花园长为80米,宽为30米,在它的四角各建有一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)种植的是不同花草.已知种植花草部分的面积为1400米2,那么矩形花园各角处的正方形观光休息亭的边长为多少米?
如图,是长清园博园内的一个矩形花园,花园长为80米,宽为30米,在它的四角各建有一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)种植的是不同花草.已知种植花草部分的面积为1400米2,那么矩形花园各角处的正方形观光休息亭的边长为多少米?