题目内容
11.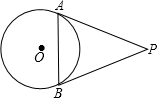 如图,PA、PB分别是⊙O的切线,切点为A、B两点.若∠P=60°,PA=4cm,则AB的长为4cm.
如图,PA、PB分别是⊙O的切线,切点为A、B两点.若∠P=60°,PA=4cm,则AB的长为4cm.
分析 由切线长定理和∠P=60°,可得△PAB为等边三角形,则AB=PA.
解答 解:∵PA,PB分别为⊙O的切线,
∴PA=PB,
∵∠P=60°,
∴△PAB为等边三角形,
∴AB=PA,
∵PA=4cm,
∴AB=4cm.
故答案为:4cm.
点评 本题考查了等边三角形的判定和切线长定理,是基础知识比较简单.

练习册系列答案
相关题目
2.如果|a+1|+(b-2)2=0,则(a+b)2015+a2的值为( )
| A. | 0 | B. | 2 | C. | -2 | D. | 1 |
6.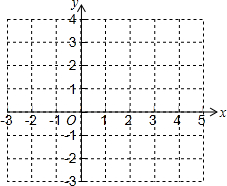 对于抛物线y=x2-4x+3.
对于抛物线y=x2-4x+3.
(1)它与x轴交点的坐标为(1,0),(3,0),与y轴交点的坐标为(0,3);
(2)在坐标系中利用描点法画出此抛物线:
(3)根据图象说明:当x为何值时,函数y随着x的增大而增大?当x为何值时,函数y随着x的增大而减小?
 对于抛物线y=x2-4x+3.
对于抛物线y=x2-4x+3.(1)它与x轴交点的坐标为(1,0),(3,0),与y轴交点的坐标为(0,3);
(2)在坐标系中利用描点法画出此抛物线:
| x | … | … | |||||
| y | … | … |
3. 如图,下列各组条件中,不能判定△ABC≌△DEF的是( )
如图,下列各组条件中,不能判定△ABC≌△DEF的是( )
 如图,下列各组条件中,不能判定△ABC≌△DEF的是( )
如图,下列各组条件中,不能判定△ABC≌△DEF的是( )| A. | AB=DE,∠A=∠D,AC=DF | B. | ∠B=∠E,AB=DE,AC=DE | ||
| C. | ∠A=∠D,AB=DE,∠B=∠E | D. | AB=DE,BC=EF,AC=DF |
1.已知A,B,C在一条直线上,AB=10,AC=6,那么AB的中点与AC的中点的距离为( )
| A. | 8 | B. | 2或8 | C. | 2 | D. | 6 |
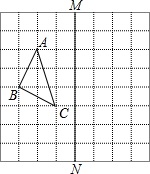 如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).