题目内容
12.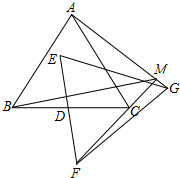 如图,△ABC、△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最大值是$\sqrt{3}$+1.
如图,△ABC、△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最大值是$\sqrt{3}$+1.
分析 取AC的中点O,连接AD、DG、BO、OM,如图,易证△DAG∽△DCF,则有∠DAG=∠DCF,从而可得A、D、C、M四点共圆,根据两点之间线段最短可得BO≤BM+OM,即BM≥BO-OM,当M在线段BO与该圆的交点处时,线段BM最长,只需求出BO、OM的值,就可解决问题.
解答 解:AC的中点O,连接AD、DG、BO、OM,如图.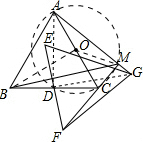
∵△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,
∴AD⊥BC,GD⊥EF,DA=DG,DC=DF,
∴∠ADG=90°-∠CDG=∠FDC,$\frac{DA}{DC}$=$\frac{DG}{DF}$,
∴△DAG∽△DCF,
∴∠DAG=∠DCF.
∴A、D、C、M四点共圆.
根据两点之间线段最短可得:BO+OM≥BM,
当M在线段BO延长线与该圆的交点处时,线段BM最长,
此时,BO=$\sqrt{B{C}^{2}-B{O}^{2}}$=$\sqrt{3}$,OM=$\frac{1}{2}$AC=1,
则BM=BO+OM=$\sqrt{3}$+1.
故答案是:$\sqrt{3}$+1.
点评 本题主要考查了旋转的性质,等边三角形的性质、等腰三角形的性质、相似三角形的判定与性质、四点共圆的判定、勾股定理、两点之间线段最短等知识,求出动点M的运动轨迹是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.小王第一天做了x个零件,第二天比第一天多做5个,第三天做的零件是第二天的2倍,若三天共做零件75个,则第一天做了( )个.
| A. | 15 | B. | 14 | C. | 10 | D. | 20 |
17.已知二次函数y=a(x+3)2-h(a≠0)有最大值1,则该函数图象的顶点坐标为( )
| A. | (-3,-1) | B. | (-3,1) | C. | (3,1) | D. | (3,-1) |
 如图所示,在一个水塘的表面均匀漂浮一些鱼食,一只小鱼正在A出,现在小鱼从A处出发到到水面取一点食物后,要回到岸边的B洞口处,画出小鱼这一过程中游动的最短路径(请保留作图中必要的辅助线).
如图所示,在一个水塘的表面均匀漂浮一些鱼食,一只小鱼正在A出,现在小鱼从A处出发到到水面取一点食物后,要回到岸边的B洞口处,画出小鱼这一过程中游动的最短路径(请保留作图中必要的辅助线).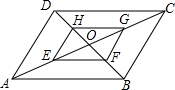 如图,?ABCD的对角线AC、BD相交于点O,点E、F、G、H分别是线段OA、OB、OC、OD的中点,那么?ABCD与四边形EFGH是否是位似图形?为什么?
如图,?ABCD的对角线AC、BD相交于点O,点E、F、G、H分别是线段OA、OB、OC、OD的中点,那么?ABCD与四边形EFGH是否是位似图形?为什么?