题目内容
3.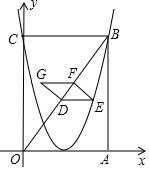 如图,在矩形OABC中,点A在x轴的正半轴,点C在y轴的正半轴.抛物线y=$\frac{16}{9}$x2-$\frac{16}{3}$x+4经过点B,C,连接OB,D是OB上的动点,过D作DE∥OA交抛物线于点E(在对称轴右侧),过E作EF⊥OB于F,以ED,EF为邻边构造?DEFG,则?DEFG周长的最大值为$\frac{243}{40}$.
如图,在矩形OABC中,点A在x轴的正半轴,点C在y轴的正半轴.抛物线y=$\frac{16}{9}$x2-$\frac{16}{3}$x+4经过点B,C,连接OB,D是OB上的动点,过D作DE∥OA交抛物线于点E(在对称轴右侧),过E作EF⊥OB于F,以ED,EF为邻边构造?DEFG,则?DEFG周长的最大值为$\frac{243}{40}$.
分析 将x=0代入二次函数解析式求出点C的坐标,根据对称性即可找出点B的坐标,由点O、B的坐标利用待定系数法即可求出直线OB的解析式,在Rt△OAB中,利用勾股定理可求出OB的长度,由DE∥OA即可得出∠BOA=∠EDF,进而得出EF=$\frac{4}{5}$DE,利用平行四边形的周长公式可求出?DEFG周长=$\frac{18}{5}$DE,设点D的坐标为($\frac{3}{4}$m,m),则点E的坐标为($\frac{3}{4}$$\sqrt{m}$+$\frac{3}{2}$,m),再利用两点间的距离公式结合配方法即可求出DE的最大值,从而得出?DEFG周长的最大值.
解答 解:当x=0时,y=$\frac{16}{9}$x2-$\frac{16}{3}$x+4=4,
∴点C(0,4);
∵y=$\frac{16}{9}$x2-$\frac{16}{3}$x+4=4$(\frac{2}{3}x-1)^{2}$,
∴抛物线的对称轴为x=$\frac{3}{2}$,
∵四边形OABC为矩形,
∴B(3,4).
设直线OB的解析式为y=kx,
将B(3,4)代入y=kx中,
4=3k,解得:k=$\frac{4}{3}$,
∴直线OB的解析式为y=$\frac{4}{3}$x.
在Rt△OAB中,OA=3,AB=4,
∴OB=$\sqrt{O{A}^{2}+A{B}^{2}}$=5.
∵DE∥OA,
∴∠BOA=∠EDF,
∵EF⊥OB,
∴$\frac{EF}{DE}=\frac{AB}{OB}$
∴EF=$\frac{4}{5}$DE,
∴?DEFG周长=2(EF+DE)=$\frac{18}{5}$DE.
设点D的坐标为($\frac{3}{4}$m,m),则点E的坐标为($\frac{3}{4}$$\sqrt{m}$+$\frac{3}{2}$,m),
∴DE=$\frac{3}{4}$$\sqrt{m}$+$\frac{3}{2}$-$\frac{3}{4}$m=-$\frac{3}{4}$(m-$\sqrt{m}$)+$\frac{3}{2}$=-$\frac{3}{4}$$(\sqrt{m}-\frac{1}{2})^{2}$+$\frac{27}{16}$,
∴当m=$\frac{1}{4}$时,DE取最大值$\frac{27}{16}$,此时?DEFG周长取最大值$\frac{243}{40}$.
故答案为$\frac{243}{40}$.
点评 本题考查了二次函数的性质、二次函数的最值、待定系数法求正比例函数解析式、勾股定理、平行四边形的性质以及平行线的性质,根据平行四边形的性质找出?DEFG周长=$\frac{18}{5}$DE是解题的关键.

 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案 一个物体的三视图如下图所示,则该物体是( )
一个物体的三视图如下图所示,则该物体是( )| A. | 圆锥 | B. | 球 | C. | 圆柱 | D. | 长方体 |
 如图,AB∥CD,BE平分∠ABC,∠C=36°,那么∠ABE的大小是( )
如图,AB∥CD,BE平分∠ABC,∠C=36°,那么∠ABE的大小是( )| A. | 18° | B. | 24° | C. | 36° | D. | 54°. |
| A. | 3×105 | B. | 3×106 | C. | 30×105 | D. | 0.3×106 |
| A. | $\left\{\begin{array}{l}{\frac{1}{x}=3}\\{x-y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+1=3}\\{y+2=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{xy=1}\\{3x-2y=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-3y=3}\\{y=-1}\end{array}\right.$ |
| A. | 3.13×105 | B. | 3.13×106 | C. | 3.13×102 | D. | 313×104 |