题目内容
已知AB∥CD,直线MN分别交AB,CD于点E,F,EG平分∠BEF交CD于点G,FH平分∠EFD交EG于点H,KG⊥EG交MN于点K,
(1)求证:FH∥KG;
(2)在(1)的条件下,连接HK,R为KG上一点,∠RHK=∠FHK,HP平分∠EHR交MN于点P,求∠PHK的度数.
(1)求证:FH∥KG;
(2)在(1)的条件下,连接HK,R为KG上一点,∠RHK=∠FHK,HP平分∠EHR交MN于点P,求∠PHK的度数.
考点:平行线的判定与性质
专题:
分析:(1)由平行线的性质和角平分线的定义可求得∠HEF+∠HFE=90°,可得∠EHF=∠HGK,可证明FH∥KG;
(2)如图2,结合平行的性质及角平分线的定义可求得可求得∴∠PHR=
∠EHR=45°+∠2,又∠PHR=∠1+∠2+∠3,可求得∠1+∠2的度数,可求得∠PHK.
(2)如图2,结合平行的性质及角平分线的定义可求得可求得∴∠PHR=
| 1 |
| 2 |
解答:(1)证明:如图1,

∵AB∥CD,
∴∠BEF+∠DFE=180°,
∵EG平分∠BEF,FH平分∠DFE,
∴∠BEF=2∠HEF,∠DFE=2∠HFE,
∴2∠HEF+2∠HFE=180°,
∴∠HEF+∠HFE=90°,
∴∠EHF=90°,
∵KG⊥EG,
∴∠KGH=∠EHF=90°,
∴FH∥KG;
(2)解:如图2,

由(1)∠FHG=∠EHF=90°,且∠2=∠3,
∴∠RHG=90°-2∠2,
∴∠EHR=180°-∠RHG=180°-(90°-2∠2)=90°+2∠2,
∴∠PHR=
∠EHR=45°+∠2,又∠PHR=∠1+∠2+∠3,
∴∠1+∠2+∠3=45°+∠2,
∴∠1+∠3=45°,
∴∠1+∠2=45°,即∠PHK=45°.

∵AB∥CD,
∴∠BEF+∠DFE=180°,
∵EG平分∠BEF,FH平分∠DFE,
∴∠BEF=2∠HEF,∠DFE=2∠HFE,
∴2∠HEF+2∠HFE=180°,
∴∠HEF+∠HFE=90°,
∴∠EHF=90°,
∵KG⊥EG,
∴∠KGH=∠EHF=90°,
∴FH∥KG;
(2)解:如图2,

由(1)∠FHG=∠EHF=90°,且∠2=∠3,
∴∠RHG=90°-2∠2,
∴∠EHR=180°-∠RHG=180°-(90°-2∠2)=90°+2∠2,
∴∠PHR=
| 1 |
| 2 |
∴∠1+∠2+∠3=45°+∠2,
∴∠1+∠3=45°,
∴∠1+∠2=45°,即∠PHK=45°.
点评:本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.

练习册系列答案
相关题目
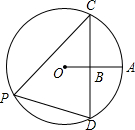 如图,点B是⊙O的半径OA的中点,且弦CD⊥OA于B,则tan∠CPD的值为( )
如图,点B是⊙O的半径OA的中点,且弦CD⊥OA于B,则tan∠CPD的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列图形:线段、正三角形、平行四边形、矩形、菱形、正方形、等腰梯形、直角梯形,其中既是中心对称图形,又是轴对称图形的共有( )
| A、3个 | B、4个 | C、5个 | D、6个 |
我校一位同学从2015年元月1号开始每天记录当天的最低气温,然后绘成统计图,为了直观反应气温的变化情况,他应选择( )
| A、折线图 | B、扇形图 |
| C、条形图 | D、以上都合适 |
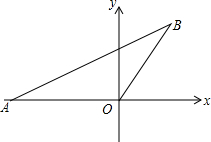 如图,OA=OB,点A的坐标是(-2,0),OB与x轴正方向夹角为60°,请画出过A,O,B三点的圆,写出圆心的坐标是
如图,OA=OB,点A的坐标是(-2,0),OB与x轴正方向夹角为60°,请画出过A,O,B三点的圆,写出圆心的坐标是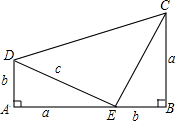 如图所示,△ADE≌△BEC,∠A=∠B=90°,A,D,B三点在一条直线上,借助这个图形,你能用面积法来验证勾股定理吗?
如图所示,△ADE≌△BEC,∠A=∠B=90°,A,D,B三点在一条直线上,借助这个图形,你能用面积法来验证勾股定理吗?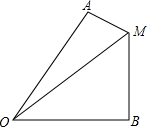 如图,已知∠AOB=60°,MA⊥OA于点A,MB⊥OB于点B,MA=2,MB=11,求OM的长.
如图,已知∠AOB=60°,MA⊥OA于点A,MB⊥OB于点B,MA=2,MB=11,求OM的长. 如图,Rt△ABC中,∠C=90°,AC=3,BC=4,以C点为圆心,CA为半径的圆与AB,BC分别交于点D,E,则弦AD的长为
如图,Rt△ABC中,∠C=90°,AC=3,BC=4,以C点为圆心,CA为半径的圆与AB,BC分别交于点D,E,则弦AD的长为