题目内容
9.先化简,再求值:(1+$\frac{2}{x+2}$)÷$\frac{1}{{x}^{2}-4}$-(2x-3),其中x=$\sqrt{3}$.分析 原式第一项括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分后去括号合并得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=$\frac{x+4}{x+2}$•(x+2)(x-2)-2x+3=x2-5,
当x=$\sqrt{3}$时,原式=3-5=-2.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19. 如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )
如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )
 如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )
如图,欲测量内部无法到达的古塔相对两点A,B间的距离,可延长AO至C,使CO=AO,延长BO至D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可测得A,B间的距离,其全等的根据是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
20.下列判断正确的是( )
| A. | 点(-2,6)与点(2,6)关于x轴对称 | B. | 点(2,-6)与点(-2,6)关于y轴对称 | ||
| C. | 点(2,6)与点(2,-6)关于x轴对称 | D. | 点(2,-6)与点(6,2)关于y轴对称 |
17.下列说法错误的是( )
| A. | 四条边都相等的四边形是菱形 | |
| B. | 有三个角是直角的四边形是矩形 | |
| C. | 对角线互相垂直平分且相等的四边形是正方形 | |
| D. | 一组对边平行,另一组对边相等的四边形是等腰梯形 |
14.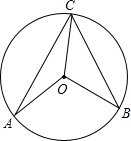 如图,A、B、C、是⊙O上的三点,且∠CAO=25°,∠BCO=35°,则∠AOB的度数为( )
如图,A、B、C、是⊙O上的三点,且∠CAO=25°,∠BCO=35°,则∠AOB的度数为( )
 如图,A、B、C、是⊙O上的三点,且∠CAO=25°,∠BCO=35°,则∠AOB的度数为( )
如图,A、B、C、是⊙O上的三点,且∠CAO=25°,∠BCO=35°,则∠AOB的度数为( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
19.点A、B是数轴上的两个点,若AB=2,点A表示的数是$-\frac{3}{2}$,则点B表示的数是( )
| A. | 2 | B. | -2 | C. | -$\frac{7}{2}$或$\frac{1}{2}$ | D. | 2或-2 |
 如图,在平行四边形ABCD中,O1、O2、O3分别是对角线BD上的三点,且BO1=O1O2=O2O3=O3D,连接AO1并延长交BC于点E,连接EO3并延长交AD于点F,则BE:DF等于8:1.
如图,在平行四边形ABCD中,O1、O2、O3分别是对角线BD上的三点,且BO1=O1O2=O2O3=O3D,连接AO1并延长交BC于点E,连接EO3并延长交AD于点F,则BE:DF等于8:1.