题目内容
2.如图1,已知线段AB两个端点坐标分别为A(a,1),B(-2,b),且a、b满足:$\sqrt{a+5}$+$\sqrt{b-3}$=0(1)则a=-5,b=3;
(2)在y轴上是否存在点C,使S△ABC=8?若存在,请求出点C的坐标;若不存在,请说明理由;
(3)如图2,将线段BA平移得到线段OD,其中B点对应O点,A点对应D点,点P(m,n)是线段OD上任意一点,求证:3n-2m=0.

分析 (1)根据题意可得a=-5,b=3;
(2)过点A作AN⊥y轴于N,过点B作BM⊥y轴于M,根据点A、B的坐标得出BM=2,OM=3,MN=2,AN=5,然后分两种情况①当C在P点的上方时;②当C在P点的下方时,使S△ABC=8,求出点C的坐标;
(3)过D点作DH⊥y轴于H,过点P作PG⊥y轴于G,可得线段OD是由线段BA向右平移2个单位,向下平移3个单位得到的,根据点P(m,n),可得PG=-m,OG=-n,DH=3,OH=2,根据S△ODH=S△OPG+S梯形PGHD,代入即可证明.
解答 解:(1)∵a、b满足:$\sqrt{a+5}$+$\sqrt{b-3}$=0,
∴a+5=0,b-3=0,
∴a=-5,b=3;
(2)过点A作AN⊥y轴于N,过点B作BM⊥y轴于M,如图1所示,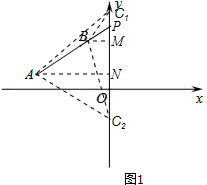
∵B(-2,3),A(-5,1),
∴BM=2,OM=3,MN=2,AN=5,
设直线AB交y轴于P,
①当C在P点的上方时,
设C1M=a,
∴S△ABC=S△ANC-S梯形ABMN-S△MBC,
∴$\frac{1}{2}$×(2+a)×5-$\frac{1}{2}$×(2+5)×2-$\frac{1}{2}$×2 a=8,
∴a=$\frac{20}{3}$,
∴C1O=a+3=$\frac{29}{3}$,
∴C1:(0,$\frac{29}{3}$),
设PM=m,
∵S△APN=S△BPM+S梯形ABMN,
∴$\frac{1}{2}$×(2+m)×5=$\frac{1}{2}$×m×2+$\frac{1}{2}$×(2+5)×2,
解得:m=$\frac{4}{3}$,
∴OP=OM+PM=$\frac{13}{3}$,
∴P(0,$\frac{13}{3}$);
②当C在P点的下方时,作点C2使PC1=PC2,
∵S△APC1=S△APC2,
S△BPC1=S△BPC2,
∴S△ABC1=S△ABC2,
∵P:(0,$\frac{13}{3}$),C1:(0,$\frac{29}{3}$),
∴PC1=PC2=$\frac{16}{3}$,
∴OC2=1,
∴C2(0,-1),
∴在y轴上存在点C,使S△ABC=8,点C的坐标分别是:C1(0,$\frac{29}{3}$),C2(0,-1);
(3)过D点作DH⊥y轴于H,过点P作PG⊥y轴于G,如图2所示,
∵点B及其对应点O的坐标分别是B(-2,3),O(0,0),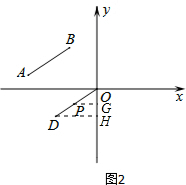
∴线段OD是由线段BA向右平移2个单位,向下平移3个单位得到的,
∴点A(-5,1)的对应点D的坐标是(-3,-2),
∵点P(m,n),
∴PG=-m,OG=-n,DH=3,OH=2,
∴S△ODH=S△OPG+S梯形PGHD,
∴$\frac{1}{2}$×3×2=$\frac{1}{2}$×(-m+3)×(n+2)+$\frac{1}{2}$×mn,
∴6=mn-mn-2m+3n+6,
∴3n-2m=0.
故答案为:-5,3.
点评 本题考查了几何变换综合题,涉及了非负数的有意义的条件,三角形和梯形的面积公式,平移的性质等知识点,解答本题的关键是根据题意作出合适的辅助线,注意分情况讨论求出点的坐标,本题综合性较强,难度适中.

 ABC考王全优卷系列答案
ABC考王全优卷系列答案 如图,直线a∥b,直线c与直线a,b都相交,∠1=65°,则∠2的度数为( )
如图,直线a∥b,直线c与直线a,b都相交,∠1=65°,则∠2的度数为( )| A. | 60° | B. | 125° | C. | 115° | D. | 65° |
 如图,直线AB、CD相交于O点,∠AOC与∠AOD的度数比为4:5,OE⊥AB,OF平分∠DOB,求∠EOF的度数.
如图,直线AB、CD相交于O点,∠AOC与∠AOD的度数比为4:5,OE⊥AB,OF平分∠DOB,求∠EOF的度数. 如图,将矩形ABCD沿EF折叠,使点D与点B重合,已知AB=3,AD=9,则BE的长为5.
如图,将矩形ABCD沿EF折叠,使点D与点B重合,已知AB=3,AD=9,则BE的长为5. 如图,每个网格都是边长为1个单位的小正方形,△ABC的每个顶点都在网格的格点上,且∠C=90°,AC=3,BC=4.
如图,每个网格都是边长为1个单位的小正方形,△ABC的每个顶点都在网格的格点上,且∠C=90°,AC=3,BC=4. 如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两
如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两 如图△BCD中,BD=CD,作CD的垂直平分线AE,交BD的延长线于A,连结AC,已知△ACD的周长为30cm,△ABC的周长为48cm,则BC长为:18.
如图△BCD中,BD=CD,作CD的垂直平分线AE,交BD的延长线于A,连结AC,已知△ACD的周长为30cm,△ABC的周长为48cm,则BC长为:18.