题目内容
9.一个三位正整数M,其各位数字均不为零且互不相等.若将M的十位数字与百位数字交换位置,得到一个新的三位数,我们称这个三位数为M的“友谊数”,如:168的“友谊数”为“618”;若从M的百位数字、十位数字、个位数字中任选两个组成一个新的两位数,并将得到的所有两位数求和,我们称这个和为M的“团结数”,如:123的“团结数”为12+13+21+23+31+32=132.(1)求证:M与其“友谊数”的差能被15整除;
(2)若一个三位正整数N,其百位数字为2,十位数字为a、个位数字为b,且各位数字互不相等(a≠0,b≠0),若N的“团结数”与N之差为24,求N的值.
分析 (1)根据题意可以表示出M的友谊数,然后作差再除以15即可解答本题;
(2)根据题意可以表示出N和N的团结数,然后作差即可解答本题.
解答 解:(1)由题意可得,
设M为100a+10b+c,则它的友谊数为:100b+10a+c,
(100a+10b+c)-(100b+10a+c)
=100a+10b+c-100b-10a-c
=100(a-b)+10(b-a)
=90(a-b),
∵$\frac{90(a-b)}{15}=6(a-b)$,
∴M与其“友谊数”的差能被15整除;
(2)由题意可得,
N=2×100+10a+b=200+10a+b,
N的团结数是:10×2+a+10a+2+10×2+b+10×b+2+10a+b+10b+a=22a+22b+44,
∴22a+22b+44-(200+10a+b)=24,
解得,$\left\{\begin{array}{l}{a=8}\\{b=4}\end{array}\right.$或$\left\{\begin{array}{l}{a=1}\\{b=8}\end{array}\right.$,
即N是284或218.
点评 本题考查因式分解的应用、解二元一次方程,解答本题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
4.若|x2-4x+4|与$\sqrt{2x-y-3}$互为相反数,则x+y的值为( )
| A. | 3 | B. | 4 | C. | 6 | D. | 9 |
17.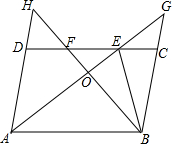 如图,在?ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论错误的是( )
如图,在?ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论错误的是( )
 如图,在?ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论错误的是( )
如图,在?ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论错误的是( )| A. | BO=OH | B. | DF=CE | C. | DH=CG | D. | AB=AE |
4.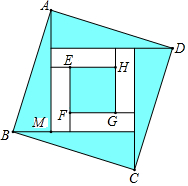 四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2$\sqrt{2}$EF,则正方形ABCD的面积为( )
四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2$\sqrt{2}$EF,则正方形ABCD的面积为( )
 四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2$\sqrt{2}$EF,则正方形ABCD的面积为( )
四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2$\sqrt{2}$EF,则正方形ABCD的面积为( )| A. | 12S | B. | 10S | C. | 9S | D. | 8S |
1.2016年6月21日,京东宣布与沃尔玛达成深度战略合作,京东向沃尔玛发行近1.45亿股A类普通股,而京东则获得1号店第三方平台1号商城的主要资产,1.45亿用科学记数法表示为( )
| A. | 1.45×1010 | B. | 0.145×109 | C. | 1.45×108 | D. | 14.5×108 |
19.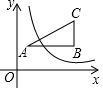 如图,△ABC的三个顶点分别为A(1,2),B(4,2),C(4,4).若反比例函数y=$\frac{k}{x}$在第一象限内的图象与△ABC有交点,则k的取值范围是( )
如图,△ABC的三个顶点分别为A(1,2),B(4,2),C(4,4).若反比例函数y=$\frac{k}{x}$在第一象限内的图象与△ABC有交点,则k的取值范围是( )
 如图,△ABC的三个顶点分别为A(1,2),B(4,2),C(4,4).若反比例函数y=$\frac{k}{x}$在第一象限内的图象与△ABC有交点,则k的取值范围是( )
如图,△ABC的三个顶点分别为A(1,2),B(4,2),C(4,4).若反比例函数y=$\frac{k}{x}$在第一象限内的图象与△ABC有交点,则k的取值范围是( )| A. | 1≤k≤4 | B. | 2≤k≤8 | C. | 2≤k≤16 | D. | 8≤k≤16 |
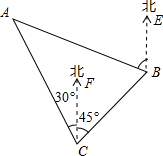 如图,A处在C处的北偏西30°方向,B处在C处的北偏东45°方向,A处在B处的北偏西70°方向,求∠BAC的度数.
如图,A处在C处的北偏西30°方向,B处在C处的北偏东45°方向,A处在B处的北偏西70°方向,求∠BAC的度数.