题目内容
19.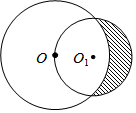 如图,一个半径为1的⊙O1经过一个半径为$\sqrt{2}$的⊙O的圆心,则图中阴影部分的面积为( )
如图,一个半径为1的⊙O1经过一个半径为$\sqrt{2}$的⊙O的圆心,则图中阴影部分的面积为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 连接OA,OB,OO1,求出∠AOB=90°,进而利用S阴影部分=S半圆AB-S弓形AB=S半圆AB-(S扇形OAB-S△OAB)=S半圆AB-S扇形OAB+S△OAB求出答案即可.
解答 解:如图,⊙O的半径为$\sqrt{2}$,⊙O1的半径为1,点O在⊙O1上,连接OA,OB,OO1,
∵OA=$\sqrt{2}$,O1A=O1O=1,则有($\sqrt{2}$)2=12+12,
∴OA2=O1A2+O1O2,
∴△OO1A为直角三角形,
∴∠AOO1=45°,同理可得∠BOO1=45°,
∴∠AOB=90°,
∴AB为⊙O1的直径.
∴S阴影部分=S半圆AB-S弓形AB=S半圆AB-(S扇形OAB-S△OAB)=S半圆AB-S扇形OAB+S△OAB=$\frac{1}{2}$π×12-$\frac{90π×2}{360}$+$\frac{1}{2}$×$\sqrt{2}$×$\sqrt{2}$=1.
故选A.
点评 本题主要考查了相交两圆的性质以及扇形面积的计算,解题的关键是正确作出辅助线,此题有一定的难度.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
9. 如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误的是( )
如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误的是( )
 如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误的是( )
如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误的是( )| A. | 4+4-$\sqrt{4}$=6 | B. | 4+40+40=6 | C. | 4+$\root{3}{4+4}$=6 | D. | 4-1÷$\sqrt{4}$+4=6 |
10.下列命题中,是真命题的是( )
| A. | 相等的角是对顶角 | |
| B. | 和为180°的两个角是邻补角 | |
| C. | 两条直线被第三条直线所截,同位角相等 | |
| D. | 过直线外一点,有且只有一条直线与已知直线平行 |
7.植树节这天,35名同学共栽了90棵树苗,其中男生每人栽3棵,女生每人栽2棵.若设男生有x人,女生有y人,则下列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=35}\\{2x+3y=90}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=35}\\{3x+2y=90}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=90}\\{2x+3y=35}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=90}\\{3x+2y=35}\end{array}\right.$ |
14.能说明“对于任何实数a,|a|>-a”是假命题的一个反例可以是( )
| A. | a=-2-1 | B. | a=$\frac{1}{3}$ | C. | a=1-3 | D. | a=π |
4.若|x2-4x+4|与$\sqrt{2x-y-3}$互为相反数,则x+y的值为( )
| A. | 3 | B. | 4 | C. | 6 | D. | 9 |
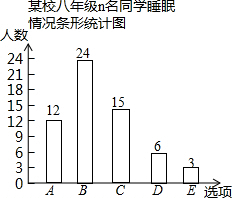 某校八年级学生会为了解本年级600名学生的睡眠情况,将同学们某天的睡眠时长t(小时)分为A,B,C,D,E(A:9≤t≤24;B:8≤t<9;C:7≤t<8;D:6≤t<7;E:0≤t<6)五个选项,进行了一次问卷调查,随机抽取n名同学的调查问卷并进行了整理,绘制成如下条形统计图,根据统计图提供的信息解答下列问题:
某校八年级学生会为了解本年级600名学生的睡眠情况,将同学们某天的睡眠时长t(小时)分为A,B,C,D,E(A:9≤t≤24;B:8≤t<9;C:7≤t<8;D:6≤t<7;E:0≤t<6)五个选项,进行了一次问卷调查,随机抽取n名同学的调查问卷并进行了整理,绘制成如下条形统计图,根据统计图提供的信息解答下列问题: 如图,AB∥CD,BE交CD于点D,CE⊥BE于点E,若∠B=34°,则∠C的大小为56度.
如图,AB∥CD,BE交CD于点D,CE⊥BE于点E,若∠B=34°,则∠C的大小为56度.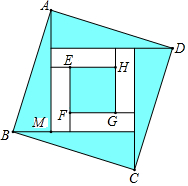 四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2$\sqrt{2}$EF,则正方形ABCD的面积为( )
四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2$\sqrt{2}$EF,则正方形ABCD的面积为( )