题目内容
 如图,△AOB中,∠O=90°,AB=5cm,OA=4cm.
如图,△AOB中,∠O=90°,AB=5cm,OA=4cm.(1)填空:OB=
(2)现将△AOB沿射线OB的方向平行移动后得到△DEF.
①当移动的距离为多少时,线段AB所扫过的面积是△AOB面积的4倍.
②当移动的距离是多少时,∠ABD是直角?
考点:平移的性质
专题:
分析:(1)由勾股定理可求得OB的长;
(2)①连接AD,则可知四边形ABFD为平行四边形,根据面积关系可求得BF和EF的关系,可得出答案;
②当∠ABD为直角时,可证明△AOB∽△BED,可求得BE的长,可求得BF,可得出答案.
(2)①连接AD,则可知四边形ABFD为平行四边形,根据面积关系可求得BF和EF的关系,可得出答案;
②当∠ABD为直角时,可证明△AOB∽△BED,可求得BE的长,可求得BF,可得出答案.
解答:解:(1)在△AOB中,∠O=90°,AB=5cm,OA=4cm,由勾股定理可求得OB=3cm,
故答案为:3;
(2)①如图,连接AD,
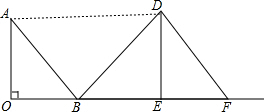
∵△AOB沿射线OB的方向平行移动后得到△DEF,
∴AB∥DF,AB=DF,AO=DE,OB=EF,
∴四边形ABFD为平行四边形,
∴S四边形ABFD=BF•DE=BF•AO=4BF,
又∵S△AOB=
OB•AO=
EF•DE=2EF,
当S四边形ABFD=4S△AOB时,则有8EF=4BF,即BF=2EF=6cm,
∴当移动的距离为6cm时,线段AB所扫过的面积是△AOB面积的4倍;
②当∠ABD为直角时,则∠ABO+∠DBE=90°,
又∵∠OAB+∠ABO=90°,
∴∠OAB=∠DBE,且∠AOB=∠∠DEB,
∴△AOB∽△BED,
∴
=
,即
=
,解得BE=
cm,
∴BF=BE+EF=
+3=
(cm),
∴当移动距离为
cm时,∠ABD为直角.
故答案为:3;
(2)①如图,连接AD,

∵△AOB沿射线OB的方向平行移动后得到△DEF,
∴AB∥DF,AB=DF,AO=DE,OB=EF,
∴四边形ABFD为平行四边形,
∴S四边形ABFD=BF•DE=BF•AO=4BF,
又∵S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
当S四边形ABFD=4S△AOB时,则有8EF=4BF,即BF=2EF=6cm,
∴当移动的距离为6cm时,线段AB所扫过的面积是△AOB面积的4倍;
②当∠ABD为直角时,则∠ABO+∠DBE=90°,
又∵∠OAB+∠ABO=90°,
∴∠OAB=∠DBE,且∠AOB=∠∠DEB,
∴△AOB∽△BED,
∴
| AO |
| BE |
| BO |
| DE |
| 4 |
| BE |
| 3 |
| 4 |
| 16 |
| 3 |
∴BF=BE+EF=
| 16 |
| 3 |
| 25 |
| 3 |
∴当移动距离为
| 25 |
| 3 |
点评:本题主要考查平移的性质及三角形相似的判定和性质,掌握平移前后的图形为全等图形是解题的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 如图,过原点的直线l与反比例函数y=-
如图,过原点的直线l与反比例函数y=-| 1 |
| x |
A、
| ||
B、2
| ||
| C、2 | ||
| D、1 |
 如图,圆O的半径为5,BC⊥OA,OD⊥AB,求OD2+CD2的值.
如图,圆O的半径为5,BC⊥OA,OD⊥AB,求OD2+CD2的值. 如图,平行四边形ABOC中,A(2,1),B(4,-3),求点C的坐标.
如图,平行四边形ABOC中,A(2,1),B(4,-3),求点C的坐标. 已知,A(n,1),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=
已知,A(n,1),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=