题目内容
19.已知一次函数y=ax+5和y=bx+3,若a>0且b<0,则这两个一次函数的图象的交点在( )| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
分析 根据k的符号来求确定一次函数y=kx+b的图象所经过的象限,然后根据a、b的情况即可求得交点的位置.
解答 解:∵一次函数y=ax+5中a>0,
∴一次函数y=ax+5的图象经过第一、二、三象限.
又∵一次函数y=bx+3中b<0,
∴一次函数y=bx+3的图象经过第一、二、四象限.
∵3<5,
∴这两个一次函数的图象的交点在第二象限,
故选C.
点评 本题主要考查两直线相交问题.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限.k<0时,直线必经过二、四象限.b>0时,直线与y轴正半轴相交.b=0时,直线过原点;b<0时,直线与y轴负半轴相交.

练习册系列答案
相关题目
9.下列计算正确的是( )
| A. | x6+x6=x12 | B. | (x2)3=x5 | C. | x-1=x | D. | x2•x3=x5 |

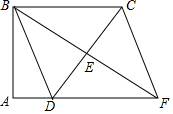 如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,点E是边CD的中点,连接BE并延长交AD的延长线于点F,连接CF.
如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,点E是边CD的中点,连接BE并延长交AD的延长线于点F,连接CF.