题目内容
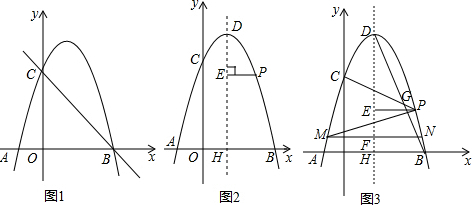
20.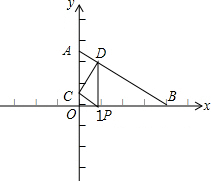 已知直角三角形纸片OAB,其中∠AOB=90°,OA=3,OB=4,点P(t,0)是OB边上的动点,过点P作PC∥AB交y轴于点C,同时过点P作PD⊥x轴交AB于点D
已知直角三角形纸片OAB,其中∠AOB=90°,OA=3,OB=4,点P(t,0)是OB边上的动点,过点P作PC∥AB交y轴于点C,同时过点P作PD⊥x轴交AB于点D(1)求直线AB的解析式并求点C的坐标(用t的代数式表示);
(2)点P在什么位置是,四边形ACPD的面积最大?最大面积是多少?
(3)点P运动过程中,△CPD是否可能是直角三角形?若可能写出此时点D的坐标;若不可能,请说明理由.
分析 (1)设出直线AB的解析式,把A、B两点坐标代入可求得其解析式,再由PC∥AB,可得∠ABO=∠CPO,再利用三角函数的定义可求得OC,可写出t的坐标;
(2)可判定四边形ACPD为平行四边形,可用t表示出AC、OP,可表示出其面积,再利用函数的性质可求得t的值及最大面积;
(3)分C和D为直角顶点,分别表示出C、P、D的坐标,再根据相似三角形的性质可得到关于t的方程,可求得t的值.
解答 解:(1)设直线AB的解析式为y=kx+b,
∵OA=3,OB=4,
∴A(0,3),B(4,0),代入解析式可得
$\left\{\begin{array}{l}{b=3}\\{4k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=3}\\{k=-\frac{3}{4}}\end{array}\right.$,
∴直线AB的解析式为y=-$\frac{3}{4}$x+3;
∵tan∠ABO=$\frac{3}{4}$,PC∥AB,
∴∠ABO=∠CPO,
∴tan∠CPO=$\frac{CO}{t}$=$\frac{3}{4}$,
∴CO=$\frac{3}{4}$t,
∴C(0,$\frac{3}{4}$t);
(2)∵AB∥CP,AC∥DP,
∴四边形ACPD是平行四边形
∵A(0,3),C(0,$\frac{3}{4}$t),P(t,0)
∴AC=3-$\frac{3}{4}$t,OP=t,
∴S四边形ACPD=AC•OP=(3-$\frac{3}{4}$t)t=-$\frac{3}{4}$(t-2)2+3,
∴当CP=2时,四边形ACPD的面积最大,它的面积是3;
(3)由题可知P不可能是直角顶点,可分两种情况:
①当点C为直角顶点时,过点D作DF⊥y轴于点F,如图1,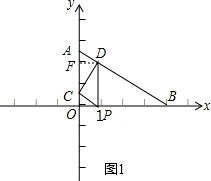
则A(0,3),C(0,$\frac{3}{4}$t),P(t,0),D(t,-$\frac{3}{4}$t+3),
∴DF=t,CO=$\frac{3}{4}$t,FC=-$\frac{3}{4}$t+3-$\frac{3}{4}$t=-$\frac{3}{2}$t+3,OP=t,
∵∠DCF+∠PCO=∠PCO+∠OPC,
∴∠DPF=∠OPC,且∠PFC=∠COP,
∴△CFD~△POC,
∴$\frac{DF}{CO}$=$\frac{FC}{OP}$,即$\frac{t}{\frac{3}{4}t}$=$\frac{-\frac{3}{2}t+3}{t}$,
解得t=$\frac{18}{17}$,则-$\frac{3}{4}$t+3=$\frac{75}{34}$,
∴D($\frac{18}{17}$,$\frac{75}{34}$);
②当点D为直角顶点时,
∵C(0,$\frac{3}{4}$t),P(t,0)
∴D(t,$\frac{3}{4}$t),
又∵D在直线AB上,把点D代入y=-$\frac{3}{4}$x+3可得$\frac{3}{4}$t=-$\frac{3}{4}$t+3,解得t=2,
∴D(2,$\frac{3}{2}$);
综上可知D点坐标为($\frac{18}{17}$,$\frac{75}{34}$)或(2,$\frac{3}{2}$).
点评 本题主要考查待定系数法求函数解析式及平行四边形的性质、相似三角形的判定和性质、二次函数的性质等知识点的综合应用.在(1)中利用平行得到∠ABO=∠CPO是解题的关键,在(2)中用t分别表示出四边形ACPD的底和高是解题的关键,在(3)中确定出点D的位置是解题的关键.本题知识点较多,综合性较强,难度适中.注意分类讨论思想和方程思想的应用.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案| A. | $\frac{2}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{7}$ |
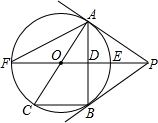 如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.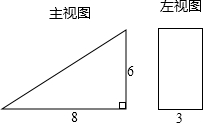 有一个几何体的形状为直三棱柱,右图是它的主视图和左视图.
有一个几何体的形状为直三棱柱,右图是它的主视图和左视图.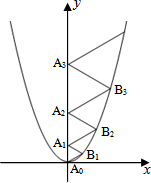 二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,A1,A2,A3,…,A2008在y轴的正半轴上,B1,B2,B3,…,B2008在二次函数y=$\frac{2}{3}$x2第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2007B2008A2008都为等边三角形,请计算△A0B1A1的边长=1;△A1B2A2的边长=2;△A2007B2008A2008的边长=2008.
二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,A1,A2,A3,…,A2008在y轴的正半轴上,B1,B2,B3,…,B2008在二次函数y=$\frac{2}{3}$x2第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2007B2008A2008都为等边三角形,请计算△A0B1A1的边长=1;△A1B2A2的边长=2;△A2007B2008A2008的边长=2008.