题目内容
15.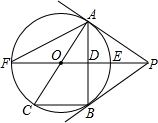 如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.(1)求证:直线PA为⊙O的切线;
(2)试探究线段OF、OD、OP之间的等量关系,并加以证明;
(3)若BC=12,tan∠F=$\frac{1}{2}$,求cos∠ACB的值和线段PE的长.
分析 (1)连接OB,通过证明△PAO和△PBO全等,得到∠PAO=∠PBO=90°,从而证明直线PA为⊙O的切线;
(2)通过证明△OAD和△OPA相似得到;
(3)设AD=x,在Rt△AOD中,通过勾股定理列方程求出AD,进而求出cos∠ACB的值和线段PE的长.
解答 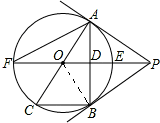 (1)证明:连接OB,
(1)证明:连接OB,
∵PB是⊙O的切线,
∴∠PBO=90°,
∵OA=OB,BA⊥PO于D,
∴AD=BD,∠POA=∠POB,
在△PAO和△PBO中,
$\left\{\begin{array}{l}{OP=OP}\\{∠POA=∠POB}\\{OA=OB}\end{array}\right.$,
∴△PAO≌△PBO(SAS),
∴∠PAO=∠PBO=90°,
∴直线PA为⊙O的切线.
(2)OF2=OD×OP.
证明:∵∠PAO=∠PDA=90°,
∴∠OAD+∠AOP=90°,∠OPA+∠AOP=90°,
∴∠OAD=∠OPA,
∴△OAD∽△OPA,
∴$\frac{OD}{OA}=\frac{OA}{OP}$,
即OA2=OD×OP,OF2=OD•OP.
(3)∵OA=OC,AD=BD,BC=12,
∴OD=$\frac{1}{2}$BC=6,
设AD=x,∵tan∠F=$\frac{1}{2}$,
∴FD=2x,OA=OF=2x-6,
在Rt△AOD中,由勾股定理,
得(2x-6)2=x2+62,
解得x1=8,x2=0(不合题意,舍去),
∴AD=8,OA=2x-6=10,
∵AC是⊙O直径,
∴∠ABC=90°,
又∵AC=2OA=20,BC=12,
∴cos∠ACB=$\frac{3}{5}$.
∴OA2=OD×OP,
∴6(PE+10)=100,
∴PE=$\frac{20}{3}$.
点评 本题综合考查了切线的判定与性质,相似,勾股定理及全等三角形的判定与性质以及锐角三角函数关系等知识,熟练掌握切线的判定与性质以及应用勾股定理列出方程是解本题的关键.

| A. | $\sqrt{9}$=±3 | B. | (-$\frac{1}{3}$)-1=-3 | C. | 2a+3b=5ab | D. | a6÷a2=a3 |
 若某几何体的三视图如图,则该几何体的全面积是(平方单位)( )
若某几何体的三视图如图,则该几何体的全面积是(平方单位)( )| A. | 78π | B. | 51π | C. | 36π | D. | 24π |
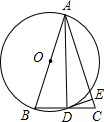 (1)如图,在△ABC中,以AB为直径的⊙O交BC于点D,连接AD,请你添加一个条件,使△ABD≌△ACD,并说明全等的理由,你添加的条件是:BD=DC.
(1)如图,在△ABC中,以AB为直径的⊙O交BC于点D,连接AD,请你添加一个条件,使△ABD≌△ACD,并说明全等的理由,你添加的条件是:BD=DC.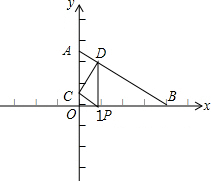 已知直角三角形纸片OAB,其中∠AOB=90°,OA=3,OB=4,点P(t,0)是OB边上的动点,过点P作PC∥AB交y轴于点C,同时过点P作PD⊥x轴交AB于点D
已知直角三角形纸片OAB,其中∠AOB=90°,OA=3,OB=4,点P(t,0)是OB边上的动点,过点P作PC∥AB交y轴于点C,同时过点P作PD⊥x轴交AB于点D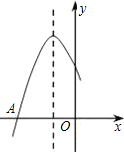 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出四个结论:①b2>4ac;②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是①④.
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出四个结论:①b2>4ac;②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是①④.