题目内容
9. 如图,C是线段AB的中点,CD=BE,CD∥BE.求证:∠D=∠E.
如图,C是线段AB的中点,CD=BE,CD∥BE.求证:∠D=∠E.
分析 由CD∥BE,可证得∠ACD=∠B,然后由C是线段AB的中点,CD=BE,利用SAS即可证得△ACD≌△CBE,继而证得结论.
解答 证明:∵C是线段AB的中点,
∴AC=CB,
∵CD∥BE,
∴∠ACD=∠B,
在△ACD和△CBE中,
$\left\{\begin{array}{l}{AC=CB}\\{∠ACD=∠B}\\{CD=BE}\end{array}\right.$,
∴△ACD≌△CBE(SAS),
∴∠D=∠E.
点评 此题考查了全等三角形的判定与性质以及平行线的性质.注意证得△ACD≌△CBE是关键.

练习册系列答案
相关题目
19.下列运算正确的是( )
| A. | x3+x=2x4 | B. | a2•a3=a6 | C. | (-2x2)3=-8x6 | D. | (x+3y)(x-3y)=x2-3y2 |
4.由于雾霾天气频发,市场上防护口罩出现热销,某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只,且所有产品当月全部售出,原料成本、销售单价及工人生产提成如表:
(1)若该公司五月份的销售收入为300万元,求甲、乙两种型号的产品分别是多少万只?
(2)公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本+生产提成总额)不超过239万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润=销售收入-投入总成本)
 | 甲 | 乙 |
| 原料成本 | 12 | 8 |
| 销售单价 | 18 | 12 |
| 生产提成 | 1 | 0.8 |
(2)公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本+生产提成总额)不超过239万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润=销售收入-投入总成本)
14.把8a3-8a2+2a进行因式分解,结果正确的是( )
| A. | 2a(4a2-4a+1) | B. | 8a2(a-1) | C. | 2a(2a-1)2 | D. | 2a(2a+1)2 |
18.下列各式,计算结果为a3的是( )
| A. | a2+a | B. | a4-a | C. | a•a2 | D. | a6÷a2 |
 请用学过的方法研究一类新函数y=$\frac{k}{{x}^{2}}$(k为常数,k≠0)的图象和性质.
请用学过的方法研究一类新函数y=$\frac{k}{{x}^{2}}$(k为常数,k≠0)的图象和性质.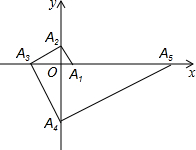 如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为-($\sqrt{3}$)2015.
如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为-($\sqrt{3}$)2015.