题目内容
9.对于平面直角坐标系xOy中的点P(m,n),定义一种变换:作点P(m,n)关于y轴对称的点P′,再将P′向左平移k(k>0)个单位得到点Pk′,Pk′叫做对点P(m,n)的k阶“?”变换.(1)求P(3,2)的3阶“?”变换后P3′的坐标;
(2)若直线y=3x-3与x轴,y轴分别交于A,B两点,点A的2阶“?”变换后得到点C,求过A,B,C三点的抛物线M的解析式;
(3)在(2)的条件下,抛物线M的对称轴与x轴交于D,若在抛物线M对称轴上存在一点E,使得以E,D,B为顶点的三角形是等腰三角形,求点E的坐标.
分析 (1)根据点P(m,n)的k阶“?”变换的定义求解;
(2)先根据坐标轴上点的坐标特征求出A(1,0),B(0,-3),再根据新定义求出C(-3,0),然后利用交点式求抛物线解析式;
(3)根据二次函数的性质求出抛物线的对称轴为直线x=-$\frac{2}{2}$=-1,可得到D(-1,0),利用勾股定理计算出BD=$\sqrt{10}$,然后分类讨论:当DB=DE=$\sqrt{10}$,如图,易得E点坐标为(-1,$\sqrt{10}$)和(-1,-$\sqrt{10}$);当BD=BE,如图,利用对称易得E点坐标为(-1,-6);若ED=EB,如图,设E(-1,t),利用两点间的距离公式得到t2=(-1)2+(t+3)2,解得t=-$\frac{5}{3}$,于是可得此时E点坐标为(-1,-$\frac{5}{3}$).
解答 解:(1)由3阶“?”变换定义:P(3,2)关于y轴对称的点为P'的坐标为(-3,2),再将P'(-3,2)向左平移3个单位得P3'的坐标P3'(-6,2);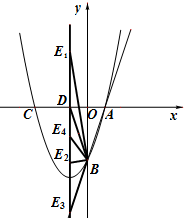
(2)当y=0,3x-3=0,解得x=1,则A(1,0);当x=0,y=3x-3=-3,则B(0,-3);
由2阶“?”变换定义:A(1,0)关于y轴对称的点为A'的坐标为(-1,0),再将A'(-1,0)向左平移2个单位得P3'的坐标A3'(-3,0),则C(-3,0);
设过A,B,C三点的抛物线M的解析式y=a(x+3)(x-1),
将B(0,-3)代入得a•3•(-1)=-3,解得a=1,
所以抛物线M的解析式为y=(x+3)(x-1)=x2+2x-3;
(3)抛物线的对称轴为直线x=-$\frac{2}{2}$=-1,则D(-1,0),
而B(0,-3),
∴BD=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
若DB=DE=$\sqrt{10}$,如图,则E1(-1,$\sqrt{10}$),E2(-1,-$\sqrt{10}$),
若BD=BE,如图,则E3(-1,-6);
若ED=EB,如图,E4B=E4D,设E4(-1,t),
则t2=(-1)2+(t+3)2,解得t=-$\frac{5}{3}$,则E4(-1,-$\frac{5}{3}$),
综上所述,点E的坐标为(-1,$\sqrt{10}$)、(-1,-$\sqrt{10}$)、(-1,-6)、(-1,-$\frac{5}{3}$).
点评 本题考查了二次函数的综合题:熟练掌握二次函数的性质和等腰三角形的性质;会利用待定系数法求二次函数的解析式;理解坐标与几何图形性质;会运用分类讨论的思想解决数学问题.

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案| x | -4.1 | -4.2 | -4.3 | -4.4 |
| x2+2x-k | -1.39 | -0.76 | -0.11 | 0.56 |
| A. | -4.1 | B. | -4.2 | C. | -4.3 | D. | -4.4 |
| A. | 倒数 | B. | 绝对值 | C. | 平方根 | D. | 相反数 |
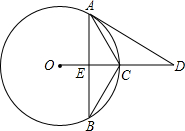 如图,△ABC内接于⊙O,OC⊥AB于点E,点D在OC的延长线上,且∠B=∠D=30°.
如图,△ABC内接于⊙O,OC⊥AB于点E,点D在OC的延长线上,且∠B=∠D=30°.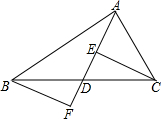 如图:在△ABC中,点D为BC边上的中点,连接AD,点E为线段AD上的一点,连接CE,过点B作BF∥CE交AD的延长线于点F,求证:CE=BF.
如图:在△ABC中,点D为BC边上的中点,连接AD,点E为线段AD上的一点,连接CE,过点B作BF∥CE交AD的延长线于点F,求证:CE=BF.