题目内容
3.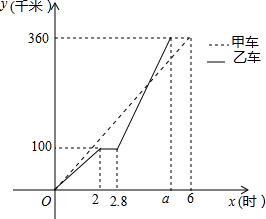 甲、乙两车同时从A地前往B地,乙行驶途中有一次停车修理,修好后乙车的行驶速度是原来的2倍,两车行驶路程y(千米)与行驶时间x(时)的函数图象如图所示,
甲、乙两车同时从A地前往B地,乙行驶途中有一次停车修理,修好后乙车的行驶速度是原来的2倍,两车行驶路程y(千米)与行驶时间x(时)的函数图象如图所示,(1)求乙车到达B地所用的时间a的值;
(2)行驶过程中,出发多长时间两车首次相遇?
(3)当x=3时,求甲、乙两车之间的距离.
分析 (1)根据函数图象可以设出在2.8≤x≤a时乙车对应的函数解析式,从而可以求得a的值;
(2)根据函数图象求出在0≤x≤6时,甲车对应的函数解析式然后与乙车对应的函数解析式联立方程组,从而可以解答本题;
(3)将x=3分别代入甲车和乙车对应的函数解析式,从而可以解答本题.
解答 解:(1)当0≤x≤2时,设乙车在这段时间内对应的函数解析式为:y=kx.
∵点(2,100)在y=kx上,
∴100=2k,
得k=50,
∴当2.8≤x≤a时设乙车对应的函数解析式为:y=100x+b.
∵点(2.8,100)在y=100x+b上,
∴100=100×2.8+b,
解得,b=-180,
∴y=100x-180.
将y=360代入y=100x-180,得x=5.4.
即a的值是5.4.
答:乙车到达B地所用的时间a的值为5.4小时;
(2)当0≤x≤6时,设甲车对应的函数的解析式为:y=mx
∵点(6,360)在y=mx上,
∴360=6m
得m=60
∴y=60x
由图象可知甲乙两车相遇在2.8≤x≤5.4之间
∴$\left\{\begin{array}{l}{y=60x}\\{y=100x-180}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4.5}\\{y=270}\end{array}\right.$,
即行驶过程中,两车出发4.5小时时两车首次相遇;
(3)将x=3代入y=60x得,y=180;
将x=3代入y=100x-180得,y=120.
180-120=60.
即当x=3时,甲、乙两车之间的距离是60千米.
点评 本题考查了一次函数的应用以及二元一次方程组的解法等知识,解题的关键是明确题意,利用数形结合的数学思想解答问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.下列计算正确的是( )
| A. | a2+a2=a4 | B. | a6÷a3=a2 | C. | 4x3-3x2=1 | D. | (-2x2y)3=-8x6y3 |
18.某班同学在探究弹簧长度跟外力的关系变化时,实验记录得到的数据如表:
则y关于x的函数图象是( )
| 砝码的质量(x克) | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
| 指针位置(y厘米) | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.5 | 7.5 |
| A. | 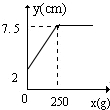 | B. | 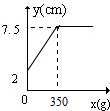 | C. | 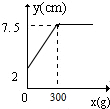 | D. |  |
 如过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图所示的几何体,其正确的展开图为( )
如过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图所示的几何体,其正确的展开图为( )



 如图,a∥b,一块等腰直角三角板的直角顶点落在直线b上,一个锐角顶点落在直线a上,若∠1=25°,则∠2=65°.
如图,a∥b,一块等腰直角三角板的直角顶点落在直线b上,一个锐角顶点落在直线a上,若∠1=25°,则∠2=65°.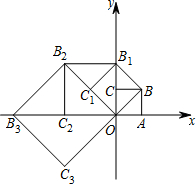 如图,在平面直角坐标系中有一被称为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2020的坐标为(-21010,-21010).
如图,在平面直角坐标系中有一被称为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2020的坐标为(-21010,-21010). 如图,在⊙O中,AB为直径,D、E为圆上两点,C为圆外一点,且∠E+∠C=90°.
如图,在⊙O中,AB为直径,D、E为圆上两点,C为圆外一点,且∠E+∠C=90°.