题目内容
9.若关于x的一元二次方程ax2+2x-$\frac{1}{2}$=0(a<0)有两个不相等的实数根,则a的取值范围是( )| A. | a<-2 | B. | a>-2 | C. | -2<a<0 | D. | -2≤a<0 |
分析 由关于x的一元二次方程ax2+2x-$\frac{1}{2}$=0(a<0)有两个不相等的实数根可得△=b2-4ac=22-4×a×(-$\frac{1}{2}$)=4+2a>0,解不等式即可求出a的取值范围.
解答 解:∵关于x的一元二次方程ax2+2x-$\frac{1}{2}$=0(a<0)有两个不相等的实数根,
∴△=b2-4ac=22-4×a×(-$\frac{1}{2}$)=4+2a>0,
解得:a>-2,
∵a<0,
∴-2<a<0.
故选C.
点评 此题考查了根的判别式.一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.同时考查了一元二次方程的定义.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
19. 如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,则∠AOB的度数为( )
如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,则∠AOB的度数为( )
 如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,则∠AOB的度数为( )
如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,则∠AOB的度数为( )| A. | 14° | B. | 28° | C. | 32° | D. | 40° |
17.下列命题中真命题有几个( )
①三角形的任意两边之和都大于第三边;②三角形的任意两角之和都大于第三个角;
③同位角都相等;④若a=b,则|a|=|b|;⑤相等的角都是直角;
⑥同角的补角不一定相等;⑦一个三角形中最大的角不会小于60°.
①三角形的任意两边之和都大于第三边;②三角形的任意两角之和都大于第三个角;
③同位角都相等;④若a=b,则|a|=|b|;⑤相等的角都是直角;
⑥同角的补角不一定相等;⑦一个三角形中最大的角不会小于60°.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.下列图形中,属于中心对称图形的是( )
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 菱形 | D. | 对角互补的四边形 |
1.据平凉市旅游局统计,2015年十一黄金周期间,平凉市接待游客38万人,实现旅游收入16000000元.将16000000用科学记数法表示应为( )
| A. | 0.16×108 | B. | 1.6×107 | C. | 16×106 | D. | 1.6×106 |
 如图,两条直线被三条平行线所截,若AB=4,BC=6,EF=5,则DF=$\frac{25}{3}$.
如图,两条直线被三条平行线所截,若AB=4,BC=6,EF=5,则DF=$\frac{25}{3}$.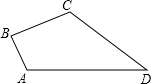 如图,在四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,则△ACD是直角三角形.
如图,在四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,则△ACD是直角三角形.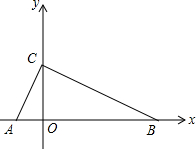 如图,已知Rt△ABC的斜边AB在x轴上,斜边上的高CO在y轴的正半轴上,且OA=1,OC=2,求经过A、B、C三点的二次函数解析式.
如图,已知Rt△ABC的斜边AB在x轴上,斜边上的高CO在y轴的正半轴上,且OA=1,OC=2,求经过A、B、C三点的二次函数解析式.