题目内容
12.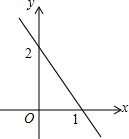 已知某个一次函数的图象如图所示,则该函数的关系式为y=-2x+2.
已知某个一次函数的图象如图所示,则该函数的关系式为y=-2x+2.
分析 设函数的解析式是y=kx+b,然后根据函数经过点(0,2)和(1,0),代入即可求解.
解答 解:设函数的解析式是y=kx+b,
则$\left\{\begin{array}{l}{b=2}\\{k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=2}\\{k=-2}\end{array}\right.$,
则函数的解析式是:y=-2x+2
点评 本题考查了待定系数法求一次函数的解析式,基本思路是先根据条件列出关于字母系数的方程,解方程求解即可得到函数解析式.当已知函数解析式时,求函数中字母的值就是求关于字母系数的方程的解.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
2.下列各数组中,不能作为直角三角形三边长的是( )
| A. | 3,$\sqrt{2},\sqrt{7}$ | B. | 3,4,5 | C. | 6,8,10 | D. | 4,5,7 |
7.在△ABC中,若sinA=$\frac{1}{2}$,则△ABC的形状是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 不能确定 |
4.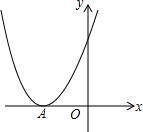 已知二次函数y=ax2+bx+c(a<0)的图象如图,当-5≤x≤0时,下列说法正确的是( )
已知二次函数y=ax2+bx+c(a<0)的图象如图,当-5≤x≤0时,下列说法正确的是( )
 已知二次函数y=ax2+bx+c(a<0)的图象如图,当-5≤x≤0时,下列说法正确的是( )
已知二次函数y=ax2+bx+c(a<0)的图象如图,当-5≤x≤0时,下列说法正确的是( )| A. | 有最小值-5、最大值0 | B. | 有最小值-3、最大值6 | ||
| C. | 有最小值0、最大值6 | D. | 有最小值2、最大值6 |
1.某商场在促销期间规定:商场对所有商品按标价的80%出售.同时当顾客在该商场消费满一定金额后,按如下方案获得响应金额的奖券:
根据上述促销方法,顾客在商场内购物可以获得双重的优惠额=折扣所享金额+奖券金额;设购买商品得到的优惠率=购买商品获得优惠额÷商品的标价.问:
(1)购买一件标价为1000元的商品,获得的优惠额为多少?优惠率是多少?
(2)对于标价在500元到800元之间(含500元和800元)的商品,顾客购买标价为多少元的商品,可以得到三分之一的优惠率?
| 消费金额a(元)的范围 | 200≤a<400 | 400≤a<500 | 500≤a<700 | 700≤a<900 | … |
| 获得奖券的金额 | 30 | 60 | 100 | 130 | … |
(1)购买一件标价为1000元的商品,获得的优惠额为多少?优惠率是多少?
(2)对于标价在500元到800元之间(含500元和800元)的商品,顾客购买标价为多少元的商品,可以得到三分之一的优惠率?
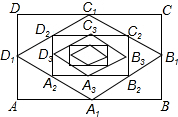 如图,在矩形ABCD中,AB=16,BC=12,顺次连结各边中点,得菱形A1B1C1D1;再顺次连结菱形A1B1C1D1的各边中点,得矩形A2B2C2D2;再顺次连结矩形A2B2C2D2的各边中点,得菱形A3B3C3D3,…这样继续下去.则图中的四边形A8B8C8D8的周长等于$\frac{7}{2}$,图中的四边形A9B9C9D9的面积等于$\frac{3}{8}$.
如图,在矩形ABCD中,AB=16,BC=12,顺次连结各边中点,得菱形A1B1C1D1;再顺次连结菱形A1B1C1D1的各边中点,得矩形A2B2C2D2;再顺次连结矩形A2B2C2D2的各边中点,得菱形A3B3C3D3,…这样继续下去.则图中的四边形A8B8C8D8的周长等于$\frac{7}{2}$,图中的四边形A9B9C9D9的面积等于$\frac{3}{8}$.