题目内容
4．
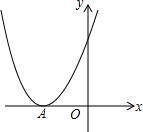已知二次函数y=ax2+bx+c（a＜0）的图象如图，当-5≤x≤0时，下列说法正确的是（ ）| A． | 有最小值-5、最大值0 | B． | 有最小值-3、最大值6 | ||
| C． | 有最小值0、最大值6 | D． | 有最小值2、最大值6 |
分析 根据二次函数的性质可判断二次函数有最小值0，则可判断C选项正确．
解答 解：因为抛物线的顶点在x轴上，抛物线开口向上，
所以二次函数有最小值0．
故选C．
点评 本题考查了二次函数的最值：当a＞0时，抛物线在对称轴左侧，y随x的增大而减少；在对称轴右侧，y随x的增大而增大，因为图象有最低点，所以函数有最小值，当x=-$\frac{b}{2a}$，y=$\frac{4ac-{b}^{2}}{4a}$；当a＜0时，抛物线在对称轴左侧，y随x的增大而增大；在对称轴右侧，y随x的增大而减少，因为图象有最高点，所以函数有最大值，当x=-$\frac{b}{2a}$，y=$\frac{4ac-{b}^{2}}{4a}$．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
14．
若反比例函数y1=$\frac{k}{x}$的图象和一次函数y2=ax+b的图象如图所示，则当y1＜y2时，相应的x的取值范围是（ ）
若反比例函数y1=$\frac{k}{x}$的图象和一次函数y2=ax+b的图象如图所示，则当y1＜y2时，相应的x的取值范围是（ ）| A． | -5＜x＜-1或x＞0 | B． | x＜-5或x＞-1 | C． | -5＜x＜-1 | D． | x＜-5或-1＜x＜0 |
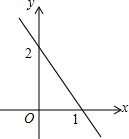已知某个一次函数的图象如图所示，则该函数的关系式为y=-2x+2．
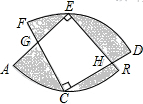如图，两个半径相等的直角扇形的圆心分别在对方的圆弧上，半径AE、CF交于点G，半径BE、CD交于点H，且C是$\widehat{AB}$的中点，若扇形的半径为4，则图中四边形EGCH的面积为8平方单位．
如图，在墙角O处有个老鼠洞，小猫在A处发现自己的“美餐”--老鼠在B处正往洞口方向逃窜，小猫马上堵截过去．若小猫与老鼠的速度相同，请你在图中画出小猫抓住老鼠的位置P．（保留作图痕迹，不写作法）