题目内容
3.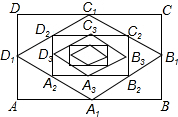 如图,在矩形ABCD中,AB=16,BC=12,顺次连结各边中点,得菱形A1B1C1D1;再顺次连结菱形A1B1C1D1的各边中点,得矩形A2B2C2D2;再顺次连结矩形A2B2C2D2的各边中点,得菱形A3B3C3D3,…这样继续下去.则图中的四边形A8B8C8D8的周长等于$\frac{7}{2}$,图中的四边形A9B9C9D9的面积等于$\frac{3}{8}$.
如图,在矩形ABCD中,AB=16,BC=12,顺次连结各边中点,得菱形A1B1C1D1;再顺次连结菱形A1B1C1D1的各边中点,得矩形A2B2C2D2;再顺次连结矩形A2B2C2D2的各边中点,得菱形A3B3C3D3,…这样继续下去.则图中的四边形A8B8C8D8的周长等于$\frac{7}{2}$,图中的四边形A9B9C9D9的面积等于$\frac{3}{8}$.
分析 根据菱形和矩形的性质、三角形中位线的性质以及勾股定理求出四边形周长和面积,得出规律求出即可.
解答 解:∵矩形ABCD中,AB=16,BC=12,顺次连结矩形形ABCD各边中点,
∴四边形A1B1C1D1是菱形,矩形对角线长=$\sqrt{1{6}^{2}+1{2}^{2}}$=20,
∴A1B1=10,
∴四边形A1B1C1D1的周长是:10×4=40,
同理可得出:A2D2=$\frac{1}{2}$BC=12×$\frac{1}{2}$=6,C2D2=$\frac{1}{2}$AB=16×6=8,
∴四边形A2B2C2D2的周长是:2(6+8)=28,
∴A4D4=3,C4D4=4,
∴四边形A4B4C4D4的周长是:2(3+4)=14,…,
∴四边形A8B8C8D8的周长=$\frac{1}{8}$×28=$\frac{7}{2}$;
根据题意得:四边形A1B1C1D1的面积=矩形ABCD面积的一半,
四边形A2B2C2D2的面积=四边形A1B1C1D1的面积的一半=$\frac{1}{4}$矩形ABCD的面积,…,
∴四边形A9B9C9D9的面积=$(\frac{1}{2})^{9}$×矩形ABCD的面积=($\frac{1}{2}$)9×16×12=$\frac{3}{8}$.
故答案为:$\frac{7}{2}$,$\frac{3}{8}$.
点评 此题主要考查了菱形的性质以及矩形的性质和中点四边形的性质等知识;根据已知得出周长和面积的变化规律是解题关键.

练习册系列答案
相关题目
13.已知⊙O的直径为10cm,点A到圆心O的距离为4,则经过点A的所以弦中,最短的弦的长为( )
| A. | 5cm | B. | 10cm | C. | 6cm | D. | 8cm |
14. 若反比例函数y1=$\frac{k}{x}$的图象和一次函数y2=ax+b的图象如图所示,则当y1<y2时,相应的x的取值范围是( )
若反比例函数y1=$\frac{k}{x}$的图象和一次函数y2=ax+b的图象如图所示,则当y1<y2时,相应的x的取值范围是( )
 若反比例函数y1=$\frac{k}{x}$的图象和一次函数y2=ax+b的图象如图所示,则当y1<y2时,相应的x的取值范围是( )
若反比例函数y1=$\frac{k}{x}$的图象和一次函数y2=ax+b的图象如图所示,则当y1<y2时,相应的x的取值范围是( )| A. | -5<x<-1或x>0 | B. | x<-5或x>-1 | C. | -5<x<-1 | D. | x<-5或-1<x<0 |
11.小聪同学对所学的部分知识进行分类,其中分类有错误的是( )
| A. |  | B. |  | C. |  | D. |  |
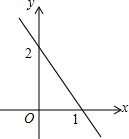 已知某个一次函数的图象如图所示,则该函数的关系式为y=-2x+2.
已知某个一次函数的图象如图所示,则该函数的关系式为y=-2x+2.