题目内容
 在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.(1)求证:△ABP≌△CAQ;
(2)请判断△APQ是什么形状的三角形?试说明你的结论.
考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)根据等边三角形的性质可得AB=AC,再根据SAS证明△ABP≌△ACQ;
(2)根据全等三角形的性质得到AP=AQ,再证∠PAQ=60°,从而得出△APQ是等边三角形.
(2)根据全等三角形的性质得到AP=AQ,再证∠PAQ=60°,从而得出△APQ是等边三角形.
解答:证明:(1)∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
在△ABP和△ACQ中,
,
∴△ABP≌△ACQ(SAS),
(2)∵△ABP≌△ACQ,
∴∠BAP=∠CAQ,AP=AQ,
∵∠BAP+∠CAP=60°,
∴∠PAQ=∠CAQ+∠CAQ=60°,
∴△APQ是等边三角形.
∴AB=AC,∠BAC=60°,
在△ABP和△ACQ中,
|
∴△ABP≌△ACQ(SAS),
(2)∵△ABP≌△ACQ,
∴∠BAP=∠CAQ,AP=AQ,
∵∠BAP+∠CAP=60°,
∴∠PAQ=∠CAQ+∠CAQ=60°,
∴△APQ是等边三角形.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了正三角形的判定,本题中求证△ABP≌△ACQ是解题的关键.

练习册系列答案
相关题目
下列说法中,正确的是( )
| A、斜边对应相等的两个直角三角形全等 |
| B、底边对应相等的两个等腰三角形全等 |
| C、面积相等的两个等边三角形全等 |
| D、面积相等的两个长方形全等 |
计算:-x2•(-x)2等于( )
| A、(-x)2+2=(-x)4=x4 |
| B、-x2•(-x)2=-x2+2=-x4 |
| C、-x2•x2=-x2+2=-x4 |
| D、-x2•x2=-x2×2=-x4 |
 某校七(1)班全体同学喜欢的球类运动如图所示的统计图表示,下面说法正确的是( )
某校七(1)班全体同学喜欢的球类运动如图所示的统计图表示,下面说法正确的是( )| A、从图中可以直接看出喜欢各种球类的具体人数 |
| B、从图中可以直接看出全班的总人数 |
| C、从图中可以直接看出全班同学一学期来喜欢各种球类的变化情况 |
| D、从图中可以直接看出全班同学现在最喜欢各种球类人数的百分比 |
 光线在不同的介质中传播的速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图所示,∠1=45°,∠2=122°.求图中其他角的度数.
光线在不同的介质中传播的速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图所示,∠1=45°,∠2=122°.求图中其他角的度数.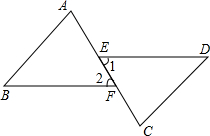 如图,已知∠A=∠C,AF=CE,DE∥BF,
如图,已知∠A=∠C,AF=CE,DE∥BF, 已知:如图,AB∥CD,AB=CD,点B、E、F、D在同一直线上,∠A=∠C.
已知:如图,AB∥CD,AB=CD,点B、E、F、D在同一直线上,∠A=∠C.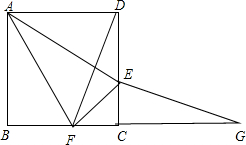 在正方形ABCD中,E、F分别是边CD、BC上的点,且CE=CF,点G是BC延长线上的一点且∠CEG+∠CDF=90°,连结EF、AE、AF.
在正方形ABCD中,E、F分别是边CD、BC上的点,且CE=CF,点G是BC延长线上的一点且∠CEG+∠CDF=90°,连结EF、AE、AF.