Question

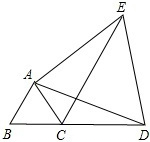如图所示，△ABC为等边三角形，D是BC延长线上一点，连接AD，以AD为边作等边△ADE．连接CE．求证：CE=AC+CD．

Answer 1

考点：全等三角形的判定与性质,等边三角形的性质

专题：证明题

分析：根据SAS即可证明△BAD≌△CAE，则CE=BD，再根据AC=BC即可证得．

解答：证明：∵△ABC是等边三角形，
∴AC=AB，∠BAC=60°．
同理，AE=AD，∠EAD=60°，
∴∠BAC=∠EAD，
∴∠BAD=∠CAE，
在△BAD和△CAE中，

AB=AC ∠BAD=∠CAE AD=AE

，
∴△BAD≌△CAE（SAS），
∴CE=BD，
又∵AC=BC，
∴CE=AC+CD．

点评：本题是全等三角形的判定与性质以及等边三角形的性质的综合应用，正确证明△BAD≌△CAE是关键．