题目内容
7．如图，将正方形ABCD的四个角向内折起，恰好拼成一个无缝无重叠的四边形EFGH，再将四边形EFGH的一个角向内折起，使点F恰好和EG的中点重合，折痕为IJ，若点H到IJ的距离HK=9cm，则边AB的长是（ ）
| A． | 16cm | B． | 12cm | C． | 9cm | D． | 6$\sqrt{2}$cm |
分析 根据翻折的对称性可知EG垂直平分FH，点K为F与EG中点连线的中点，然后根据HK的长度求出HF，即为正方形ABCD的边长，从而得解．
解答 解：∵正方形ABCD无缝隙无重叠得到四边形EFGH，
∴EG垂直平分FH，
∵四边形EFGH的一个角向内折起点F恰好和EG的中点重合，
∴点K为F与EG中点连线的中点，
∵HK=12cm，
∴HF=HK÷$\frac{3}{4}$=9÷$\frac{3}{4}$=12cm，
∴正方形ABCD的边长为12cm，
∴AB=12cm．
故选B．
点评 本题考查了翻折变换的性质，根据翻折前后的两个图形能够互相重合判断出垂直平分和中点，最后求出HF的长是解题的关键．
练习册系列答案
华东师大版一课一练系列答案
相关题目
17．计算（-3）×2的结果是（ ）
| A． | 5 | B． | -5 | C． | 6 | D． | -6 |
18．化简：$\frac{x-4}{{x}^{2}-9}$÷（1-$\frac{1}{x-3}$）的结果是（ ）
| A． | x-4 | B． | x+3 | C． | $\frac{1}{x-3}$ | D． | $\frac{1}{x+3}$ |
15．已知一个反比例函数的图象经过点A（3，-4），那么不在这个函数图象上的点是（ ）
| A． | （-3，-4） | B． | （-3，4） | C． | （2，-6） | D． | （$\frac{\sqrt{2}}{2}$，-12$\sqrt{2}$） |
2．已知△ABC∽△DEF，S△ABC：S△DEF=1：4．若BC=1，则EF的长为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
12．
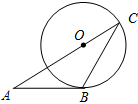如图，AB与⊙O目切于点B，连接AO，AO的延长线交⊙O于点C，连接BC，若∠A=40°，则∠C的度数为（ ）
如图，AB与⊙O目切于点B，连接AO，AO的延长线交⊙O于点C，连接BC，若∠A=40°，则∠C的度数为（ ）| A． | 50° | B． | 25° | C． | 20° | D． | 15° |
19．
已知实数m、n在数轴上的对应点的位置如图，则|m-n|+$\sqrt{1-2n+{n}^{2}}$=（ ）
已知实数m、n在数轴上的对应点的位置如图，则|m-n|+$\sqrt{1-2n+{n}^{2}}$=（ ）| A． | m-1 | B． | m+1 | C． | 2n-m+1 | D． | 2n-m-1 |