题目内容
12.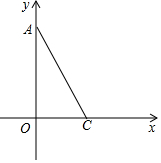 如图,在Rt△AOC中,∠A=30°,点O(0,0),C(1,0),点A在y轴正半轴上,以AC为一边作等腰直角△ACP,使得点P在第一象限.
如图,在Rt△AOC中,∠A=30°,点O(0,0),C(1,0),点A在y轴正半轴上,以AC为一边作等腰直角△ACP,使得点P在第一象限.(1)求出所有符合题意的点P的坐标;
(2)在△AOC内部存在一点Q,使得AQ、OQ、CQ之和最小,请求出这个和的最小值.
分析 (1)根据C(1,0),得到OC=1,解直角三角形得到AC=2,OA=$\sqrt{3}$,如图1,①当AC=AP,∠CAP=90°,过P1作P1B⊥y轴于B,②当AC=CP,∠ACP=90°,过P2作P2D⊥x轴于D,③当CP=AP,∠APC=90°,过P3作P3E⊥x轴于E,解直角三角形即可得到结论;
(2)任取△AOC内一点Q,连接AQ、BQ、CQ,将△ACQ绕点C顺时针旋转60°得到△A′CQ’,于是得到当A′Q′,OQ,QQ′这三条线段在同一直线时最短,即AQ+OQ+CQ的最小值=OA′,过A′作A′B⊥x轴于B,解直角三角形即可得到结论.
解答 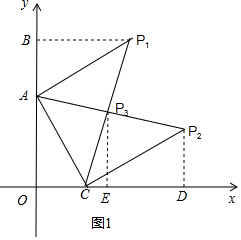 解:(1)∵C(1,0),
解:(1)∵C(1,0),
∴OC=1,
∵在Rt△AOC中,∠A=30°,
∴AC=2,OA=$\sqrt{3}$,
如图1,①当AC=AP,∠CAP=90°,过P1作P1B⊥y轴于B,
则△ABP1≌△COA,
∴AB=OC=1,BP1=AO=$\sqrt{3}$,
∴OB=1+$\sqrt{3}$,
∴P1($\sqrt{3}$,1+$\sqrt{3}$);
②当AC=CP,∠ACP=90°,过P2作P2D⊥x轴于D,
同理可得:CD=OA=$\sqrt{3}$,P2D=1,
∴P2(1+$\sqrt{3}$,1);
③当CP=AP,∠APC=90°,过P3作P3E⊥x轴于E,
则P3是AP2的中点,
∴OE=$\frac{1}{2}$OD=$\frac{1+\sqrt{3}}{2}$,P3E=$\frac{1}{2}$(OA+P2D)=$\frac{1+\sqrt{3}}{2}$,
∴P3($\frac{1+\sqrt{3}}{2}$,$\frac{1+\sqrt{3}}{2}$);
综上所述,P($\sqrt{3}$,1+$\sqrt{3}$),(1+$\sqrt{3}$,1),($\frac{1+\sqrt{3}}{2}$,$\frac{1+\sqrt{3}}{2}$);
(2)如图2,任取△AOC内一点Q,连接AQ、BQ、CQ,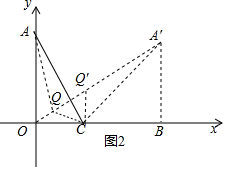
将△ACQ绕点C顺时针旋转60°得到△A′CQ’,
∴A′C=AC=2,CQ=CQ′,AQ=A′Q′,∠ACA′=∠QCQ′=60°,
∴△QCQ′是等边三角形,
∴CQ=QQ′,
∴AQ+OQ+CQ=A′Q′+OQ+QQ’,
∴当A′Q′,OQ,QQ′这三条线段在同一直线时最短,即AQ+OQ+CQ的最小值=OA′,
∵∠ACO=∠ACA′=60°,
∴∠A′CB=60°,
过A′作A′B⊥x轴于B,
∴BC=$\frac{1}{2}$A’C=1,A′B=$\sqrt{3}$,
∴OB=2,
∴A′O=$\sqrt{O{B}^{2}+A′{B}^{2}}$=$\sqrt{7}$,
∴AQ、OQ、CQ之和的最小值是$\sqrt{7}$.
点评 本题考查了轴对称-最短距离问题,等腰直角三角形的性质,坐标与图形性质,等边三角形的判定和性质,正确作出图形是解题的关键.

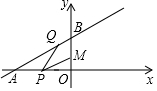 如图所示,已知点M(0,2),直线y=$\frac{\sqrt{3}}{3}$x+4与两坐标轴分别交于A,B两点,P、Q分别是线段OA,AB上的动点,则PQ+MP的最小值是3$\sqrt{3}$.
如图所示,已知点M(0,2),直线y=$\frac{\sqrt{3}}{3}$x+4与两坐标轴分别交于A,B两点,P、Q分别是线段OA,AB上的动点,则PQ+MP的最小值是3$\sqrt{3}$. | 阅读量(单位:本/周) | 0 | 1 | 2 | 3 | 4 |
| 人数 | 1 | 4 | 6 | 2 | 2 |
| A. | 中位数是2 | B. | 平均数是2 | C. | 众数是4 | D. | 方差是1.2 |
| A. | b>8 | B. | b>-8 | C. | b≥8 | D. | b≥-8 |
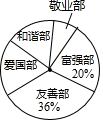 小颖为了了解2017年支付宝的“五福(友善福、敬业福、富强福、和谐福、爱国福)抽取机率,她在某微信群中进行调查(参与调查的微友每人抽取一张福卡),并将调查得到的数据用下面不完整的表和扇形图来表示.
小颖为了了解2017年支付宝的“五福(友善福、敬业福、富强福、和谐福、爱国福)抽取机率,她在某微信群中进行调查(参与调查的微友每人抽取一张福卡),并将调查得到的数据用下面不完整的表和扇形图来表示. | 福卡 | 和谐福 | 富强福 | 爱国福 | 友善福 | 敬业福 |
| 人数 | 21 | 20 | a | b | 8 |
(1)计算出表中a、b的值;
(2)求扇形统计图中表示“爱国福”部分所对应的扇形的圆心角度数;
(3)若只在这些友好之间转赠福卡,则这次最多有多少人可收集到“五福”?
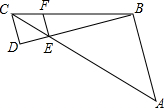 如图所示,AB∥CD∥EF,AC与BD相交于点E,若CE=4,CF=3,AE=BC,则$\frac{CD}{AB}$的值是$\frac{1}{3}$.
如图所示,AB∥CD∥EF,AC与BD相交于点E,若CE=4,CF=3,AE=BC,则$\frac{CD}{AB}$的值是$\frac{1}{3}$. 如图,菱形ABCD中,∠A=60°,BD=6,则菱形ABCD的周长为24.
如图,菱形ABCD中,∠A=60°,BD=6,则菱形ABCD的周长为24.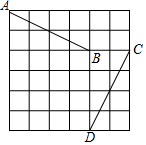 如图,A点的坐标为(-1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐标为(3,-1),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是(1,1)或(4,4).
如图,A点的坐标为(-1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐标为(3,-1),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是(1,1)或(4,4).