题目内容
 如图,已知PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,若∠PAB=40°,求∠P的度数.
如图,已知PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,若∠PAB=40°,求∠P的度数.考点:切线的性质
专题:计算题
分析:根据切线长定理得到PA=PB,根据等腰三角形的性质得∠PAB=∠PBA=40°,然后利用三角形内角和计算∠P的度数.
解答:解:∵PA、PB是⊙O的切线,
∴PA=PB,
∴∠PAB=∠PBA=40°,
∴∠P=180°-40°-40°=100°.
故答案为100°.
∴PA=PB,
∴∠PAB=∠PBA=40°,
∴∠P=180°-40°-40°=100°.
故答案为100°.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了切线长定理.

练习册系列答案
相关题目
下列说法:(1)
是单项式;(2)3是一次单项式;(3)x的次数是0;(4)-x的系数是0.其中错误的说法的个数是( )
| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
在3,-2,0.5,-1这四个数中,最小的是( )
| A、3 | B、-2 | C、0.5 | D、-1 |
 我国深潜器目前最大的深潜极限为7062.68m,某天深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.
我国深潜器目前最大的深潜极限为7062.68m,某天深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.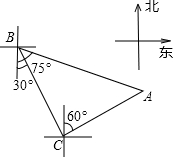 轮船从B处以每小时40海里的速度沿南偏东30°方向匀速航行,轮船航行1.5小时到达C处,在C处观测灯塔A位于北偏东60°方向上,且与C处相距80海里,则B处与灯塔A的距离是
轮船从B处以每小时40海里的速度沿南偏东30°方向匀速航行,轮船航行1.5小时到达C处,在C处观测灯塔A位于北偏东60°方向上,且与C处相距80海里,则B处与灯塔A的距离是