题目内容
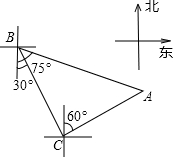轮船从B处以每小时40海里的速度沿南偏东30°方向匀速航行，轮船航行1.5小时到达C处，在C处观测灯塔A位于北偏东60°方向上，且与C处相距80海里，则B处与灯塔A的距离是考点：勾股定理的应用,方向角
专题：
分析：根据方向角得出∠BCA=90°，进而利用勾股定理得出AB的长．
解答：
解：由题意可得：BC=1.5×40=60（海里），
∠EBC=∠FCB=30°，
故∠BCA=90°，
则AB=
=
=100（海里），
故答案为：100．
解：由题意可得：BC=1.5×40=60（海里），∠EBC=∠FCB=30°，
故∠BCA=90°，
则AB=
| BC2+AC2 |
| 602+802 |
故答案为：100．
点评：此题主要考查了方向角以及勾股定理，得出∠BCA=90°是解题关键．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
某校初中一年级组建篮球队，对甲、乙两名备选同学进行定位投篮测试，每次投10个球共投10次．甲、乙两名同学测试情况如图所示：
如图，已知PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，若∠PAB=40°，求∠P的度数．下列说法正确的是（ ）
| A、任何有理数均可用分数形式表示 | ||
| B、数轴上的点与有理数一一对应 | ||
C、1和2之间的无理数只有
| ||
| D、不带根号的数都是有理数 |
关于二次函数y=2x2+3，下列说法中正确的是（ ）
| A、它的开口方向是向下 |
| B、当x＜-1时，y随x的增大而减小 |
| C、它的顶点坐标是（2，3） |
| D、当x=0时，y有最大值是3 |
下列各点中，不在一次函数y=-2x+1的图象上的是（ ）
| A、（1，-1） |
| B、（0，1） |
| C、（2，0） |
| D、（-1，3） |