题目内容
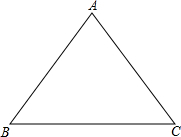如图，在△ABC中，已知AB=| 6 |
考点：勾股定理,含30度角的直角三角形,等腰直角三角形
专题：
分析：首先过点A作AD⊥BC于点D，进而利用锐角三角函数关系求出AD，BD，AC以及DC的长，即可得出答案．
解答：
解：过点A作AD⊥BC于点D，
∵AB=
，∠B=45°，
∴BD=ABsin45°=
×
=
，
∴AD=
，
∵∠C=60°，
∴AC=AD÷sin60°=2，
∴DC=1，
∴BC=
+1．
答：AC的长为2，BC的长为
+1．
解：过点A作AD⊥BC于点D，∵AB=
| 6 |
∴BD=ABsin45°=
| 6 |
| ||
| 2 |
| 3 |
∴AD=
| 3 |
∵∠C=60°，
∴AC=AD÷sin60°=2，
∴DC=1，
∴BC=
| 3 |
答：AC的长为2，BC的长为
| 3 |
点评：此题主要考查了解直角三角形的应用，熟练应用锐角三角函数关系是解题关键．
练习册系列答案
相关题目
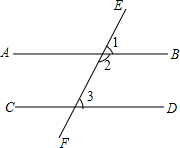已知∠2=3∠1且∠1+∠3=90°，试说明AB∥CD．