题目内容
18.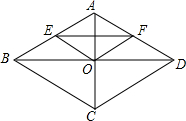 如图,菱形纸片ABCD的对角线AC、BD相交于点O,折叠纸片使点A与点O重合,折痕为EF,若AB=5,BD=8,则△OEF的面积为( )
如图,菱形纸片ABCD的对角线AC、BD相交于点O,折叠纸片使点A与点O重合,折痕为EF,若AB=5,BD=8,则△OEF的面积为( )| A. | 12 | B. | 6 | C. | 3 | D. | $\frac{3}{2}$ |
分析 根据菱形的性质得出BO=OD,AC⊥BD,根据勾股定理求出AO,根据折叠得出EF垂直平分AO,求出AE=BE,AF=DF,AM=OM,求出OM和EF长,根据三角形的面积公式即可得出答案.
解答 解:∵四边形ABCD是菱形,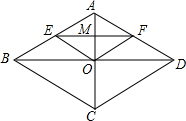
∴AC⊥BD,BO=OD=$\frac{1}{2}$BD=$\frac{1}{2}$×8=4,
∴∠AOB=90°,
在Rt△AOB中,由勾股定理得:AO=$\sqrt{A{B}^{2}-B{O}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∵折叠纸片使点A与点O重合,折痕为EF,AC⊥BD,
∴EF垂直平分AO,EF∥BD,
∴AE=BE,DF=AF,AM=OM=$\frac{1}{2}$AO=$\frac{3}{2}$,
∴EF=$\frac{1}{2}$BD=$\frac{1}{2}$×8=4,
∵EF⊥AO,
∴∠OME=90°,
∴△OEF的面积为$\frac{1}{2}$×EF×OM=$\frac{1}{2}$×4×$\frac{3}{2}$=3,
故选C.
点评 本题考查了勾股定理,三角形的中位线,菱形的性质,折叠的性质的应用,能综合 运用定理进行推理是解此题的关键,注意:菱形的对角线垂直且互相平分.

练习册系列答案
相关题目
9. 如图,在?ABCD中,AB=3,BC=5,∠ABC的平分线交AD于点E,则DE的长为( )
如图,在?ABCD中,AB=3,BC=5,∠ABC的平分线交AD于点E,则DE的长为( )
 如图,在?ABCD中,AB=3,BC=5,∠ABC的平分线交AD于点E,则DE的长为( )
如图,在?ABCD中,AB=3,BC=5,∠ABC的平分线交AD于点E,则DE的长为( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
6.在平面直角坐标系中,在第四象限内有一点P,且点P到x轴的距离是4,到y轴的距离是5,则点P的坐标为( )
| A. | (4,-5) | B. | (4,5) | C. | (-5,-4) | D. | (5,-4) |
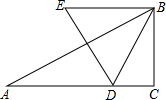 如图,己知△ABC中,∠C=90°,∠A=30°,AC=$\sqrt{3}$.动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为$\sqrt{3}$.
如图,己知△ABC中,∠C=90°,∠A=30°,AC=$\sqrt{3}$.动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为$\sqrt{3}$.