题目内容
8．
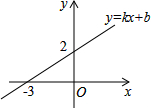一次函数y=kx+b（k，b是常数，k≠0）的图象如图所示，则不等式kx+b＞0的解集是x＞-3．
分析 不等式kx+b＞0的解集为直线y=kx+b落在x轴上方的部分对应的x的取值范围．
解答 解：从图象得知一次函数y=kx+b（k，b是常数，k≠0）的图象经过点（-3，0），并且函数值y随x的增大而增大，
因而不等式kx+b＞0的解集是x＞-3．
故答案为x＞-3．
点评 本题考查了一次函数与一元一次不等式的关系：从函数的角度看，就是寻求使一次函数y=ax+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．
练习册系列答案
相关题目
18．甲、乙两个人关于年龄有如下对话，甲说：“我是你现在这个年龄时，你是10岁”．乙说：“我是你现在这个年龄时，你是25岁”．设现在甲x岁，乙y岁，下列方程组正确的是（ ）
| A． | $\left\{\begin{array}{l}{y-10=x-y}\\{x-y=25-x}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{y-10=x-y}\\{x-y=25-y}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{y-10=x-y}\\{x-y=25+x}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{y+10=x-y}\\{x-y=25-x}\end{array}\right.$ |
19．已知关于x的不等式ax-3x+2＞5的一个解是-2，则a的取值范围为（ ）
| A． | a＜$\frac{3}{2}$ | B． | a＞$\frac{3}{2}$ | C． | a＞-$\frac{9}{2}$ | D． | a＜-$\frac{9}{2}$ |
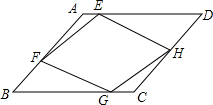菱形ABCD的边长为4，∠B=60°，F、H分别是AB、CD的中点，E、G分别在AD、BC上，且AE=CG．
3．如果（x+1）（2x+m）的乘积中不含x的一次项，则m的值为（ ）
| A． | -0.5 | B． | 0.5 | C． | -2 | D． | 2 |
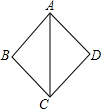如图，在△ABC和△ADC中，下列结论：