题目内容
15.使$\sqrt{{a}^{2}-6a+34}$+$\sqrt{{a}^{2}-2a+5}$取最小值的实数a的值为$\frac{4}{3}$.分析 由$\sqrt{{a}^{2}-6a+34}$+$\sqrt{{a}^{2}-2a+5}$=$\sqrt{(a-3)^{2}+{5}^{2}}$+$\sqrt{(a-1)^{2}+{2}^{2}}$,可知欲求$\sqrt{{a}^{2}-6a+34}$+$\sqrt{{a}^{2}-2a+5}$的最小值,相当于在x轴上找一点P(a,0),d到A(1,2),B(3,5)的距离之和最小.
解答 解:∵$\sqrt{{a}^{2}-6a+34}$+$\sqrt{{a}^{2}-2a+5}$=$\sqrt{(a-3)^{2}+{5}^{2}}$+$\sqrt{(a-1)^{2}+{2}^{2}}$,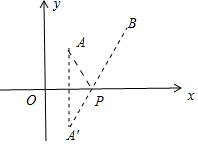
欲求$\sqrt{{a}^{2}-6a+34}$+$\sqrt{{a}^{2}-2a+5}$的最小值,相当于在x轴上找一点P(a,0),d到A(1,2),B(3,5)的距离之和最小,
作点A关于x轴的对称点A′(1,-2),连接A′B交x轴于P,点P即为所求,
易知直线A′B的解析式为y=3x-4,令y=0,解得x=$\frac{4}{3}$,
∴P($\frac{4}{3}$,0),
∴a=$\frac{4}{3}$.
故答案为$\frac{4}{3}$
点评 本题主要考查了最短路线问题,利用了数形结合的思想,通过构建一次函数求解是解题关键.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
7.在单词happy中随机选择一个字母,选到字母为p的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
20.扇形的半径扩大为原来的2倍,圆心角缩小为原来的$\frac{1}{2}$,那么扇形的面积( )
| A. | 不变 | B. | 扩大为原来的2倍 | C. | 缩小为原来的$\frac{1}{2}$ | D. | 扩大为原来的4倍 |
7.某校数学兴趣小组经过市场调查,得到某品牌书包每月的销量与售价的相关信息如下表:
已知该品牌书包的进价为每个70元,若设售价为每个x元,月销量为y件.
(1)求y与x的关系式;
(2)已知每个书包的利润不低于10元且不超过100元,问售价为多少元时,当月的销量最大,最大销量是多少?
| 售价(元/个) | 100 | 110 | 120 | 130 | … |
| 月销量(个) | 200 | 180 | 160 | 140 | … |
(1)求y与x的关系式;
(2)已知每个书包的利润不低于10元且不超过100元,问售价为多少元时,当月的销量最大,最大销量是多少?
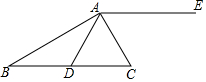 如图,在△ABC中,点D在BC边上,BD=AD=AC,AC平分∠DAE.
如图,在△ABC中,点D在BC边上,BD=AD=AC,AC平分∠DAE.