题目内容
20.扇形的半径扩大为原来的2倍,圆心角缩小为原来的$\frac{1}{2}$,那么扇形的面积( )| A. | 不变 | B. | 扩大为原来的2倍 | C. | 缩小为原来的$\frac{1}{2}$ | D. | 扩大为原来的4倍 |
分析 设原来扇形的半径为r,圆心角为n,则扇形的面积=$\frac{nπ{r}^{2}}{360}$,将扇形的半径扩大为原来的2倍,圆心角缩小为原来的$\frac{1}{2}$,那么扇形的面积为$\frac{\frac{1}{2}nπ(2r)^{2}}{360}$=2•$\frac{nπ{r}^{2}}{360}$,由此即可判断.
解答 解:设原来扇形的半径为r,圆心角为n,则扇形的面积=$\frac{nπ{r}^{2}}{360}$,
将扇形的半径扩大为原来的2倍,圆心角缩小为原来的$\frac{1}{2}$,那么扇形的面积为$\frac{\frac{1}{2}nπ(2r)^{2}}{360}$=2•$\frac{nπ{r}^{2}}{360}$,
∴面积扩大为原来的2倍,
故选B.
点评 本题考查扇形的面积的计算,灵活应用所学知识解决问题,是解题的关键.

练习册系列答案
相关题目
12.下列各数中,最小的数是( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{3}$ | C. | -$\sqrt{2}$ | D. | -$\sqrt{3}$ |
13.3-$\sqrt{5}$的绝对值是( )
| A. | 3-$\sqrt{5}$ | B. | $\sqrt{5}$-3 | C. | -3-$\sqrt{5}$ | D. | 3+$\sqrt{5}$ |
5.在平面直角坐标系中,将抛物线C1:y=x2平移后得到抛物线C2,使得抛物线C2恰好经过抛物线C1的顶点,且抛物线C2与x轴有两个交点,分别记为点A、点B.若AB=2$\sqrt{3}$,抛物线C2的顶点为点C,则△ABC的周长是( )
| A. | 3+2$\sqrt{2}$ | B. | 6+2$\sqrt{3}$ | C. | 6$\sqrt{3}$ | D. | 12$\sqrt{3}$ |
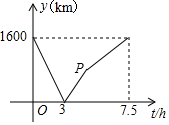 【情景】A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),相距y(km)与时间t(h)满足的数量关系如图所示.
【情景】A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),相距y(km)与时间t(h)满足的数量关系如图所示. 如图,已知?ABCD.
如图,已知?ABCD.