题目内容
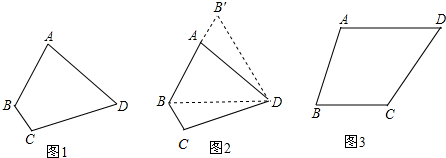
7．已知三条线段长分别为22厘米，16厘米，18厘米，以那两条为对角线，其余一条为边，可以画出平行四边形吗？进行讨论；如果以a，b为对角线，以c为一边画平行四边形的话，a，b，c间应满足什么？分析 根据平行四边形的对角线互相平分和三角形的三边关系确定答案即可．
解答 解：设对角线为a、b，边为c．
∵平行四边形对角线相互平分，
∴则$\frac{a}{2}$，$\frac{b}{2}$，c这3条线长组成一个三角形，
∵三角形两边之和大于第三边，两边之差小于第三边，
∴$\frac{a-b}{2}$＜c＜$\frac{a+b}{2}$；
则可得知：22厘米、16厘米为对角线，18厘米为边可以画出平行四边形；22cm、18cm为对角线，16cm为边，可以画出平行四边形．
点评 考查了平行四边形的判定、三角形的三边关系等知识，解题的关键是根据三边关系确定a、b、c的关系．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
17．
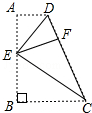如图，四边形ABCD中，AD∥BC，∠B=90°，E为AB上一点，分别以ED，EC为折痕将两个角（∠A，∠B）向内折起，点A，B恰好落在CD边的点F处．若AD=4，BC=7，则EF的值是（ ）
如图，四边形ABCD中，AD∥BC，∠B=90°，E为AB上一点，分别以ED，EC为折痕将两个角（∠A，∠B）向内折起，点A，B恰好落在CD边的点F处．若AD=4，BC=7，则EF的值是（ ）| A． | 2$\sqrt{7}$ | B． | 4$\sqrt{7}$ | C． | 2$\sqrt{6}$ | D． | 4$\sqrt{6}$ |
15．
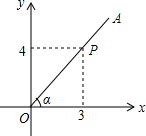如图，P是∠α的边OA上一点，且点P的坐标为（3，4），则sinα=（ ）
如图，P是∠α的边OA上一点，且点P的坐标为（3，4），则sinα=（ ）| A． | $\frac{3}{4}$ | B． | $\frac{4}{3}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
已知，如图，?ABCD中，CN=AM，AE=CF，求证：EN∥MF．