题目内容
17.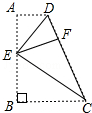 如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处.若AD=4,BC=7,则EF的值是( )
如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处.若AD=4,BC=7,则EF的值是( )| A. | 2$\sqrt{7}$ | B. | 4$\sqrt{7}$ | C. | 2$\sqrt{6}$ | D. | 4$\sqrt{6}$ |
分析 如图,首先证明DF=4,CF=7;其次证明∠DEC=90°,然后运用射影定理求出EF的长度,即可解决问题.
解答  解:如图,由翻折变换的性质得:
解:如图,由翻折变换的性质得:
DF=DA=4,CF=CB=7;
∠DEA=∠DEF,∠CEF=∠CEB,
∴∠DEC=$\frac{1}{2}$×180°=90°,
由射影定理得:EF2=CF•DF,
∴EF=2$\sqrt{7}$,
故选A.
点评 该题主要考查了翻折变换的性质、射影定理等几何知识点及其应用问题;解题的关键是牢固掌握翻折变换的性质、射影定理等几何知识点.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
12.二次函数y=2x2的图象先向右平移1个单位,再向上平移3个单位后,所得到的抛物线的表达式为( )
| A. | y=2(x+1)2+3 | B. | y=2(x+1)2-3 | C. | y=2(x-1)2+3 | D. | y=2(x-1)2-3 |
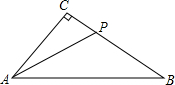 已知:如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P在BC上运动,点P不与点B,C重合,设PC=x,若用y表示△APB的面积,求y与x的函数关系式,并求自变量x的取值范围.
已知:如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P在BC上运动,点P不与点B,C重合,设PC=x,若用y表示△APB的面积,求y与x的函数关系式,并求自变量x的取值范围.