题目内容
6.一个不透明的布袋中有5个红球,12个白球,13个黄球,它们除颜色外都相同.(1)求从袋中摸出一个球是红球的概率;
(2)现从袋中取走若干个黄球,并放入相同数量的红球,搅拌均匀后,要使从袋中摸出一个球是红球的概率不小于$\frac{1}{4}$,问至少需取走了多少个黄球?
分析 (1)根据概率公式,求摸到红球的概率,即用红球的个数除以小球总个数即可得出得到红球的概率;
(2)假设取走了x个黄球,则放入x个红球,进而利用概率公式得出不等式,求出即可.
解答 解:(1)∵5个红球,12个白球,13个黄球,
∴摸出一个球摸是红球的概率为$\frac{5}{5+12+13}$=$\frac{1}{6}$;
(2)设取走x个黄球,则放入x个红球,
由题意,得$\frac{5+x}{5+12+13}$≥$\frac{1}{4}$,
解得:x≥$\frac{5}{2}$,
∵x为整数,
∴x的最小正整数解是x=3.
答:至少取走了3个黄球.
点评 此题考查了概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目
17.如果一个三角形的两边分别为2和4,则第三边长可能是( )
| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
1.现定义一种新运算“*”,规定a*b=ab+a-b,如1*3=1×3+1-3,则(-2*5)*6等于( )
| A. | 120 | B. | 125 | C. | -120 | D. | -125 |
11.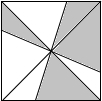 一只蚂蚁在如图所示的正方形地砖上爬行,蚂蚁停留在阴影部分的概率为( )
一只蚂蚁在如图所示的正方形地砖上爬行,蚂蚁停留在阴影部分的概率为( )
 一只蚂蚁在如图所示的正方形地砖上爬行,蚂蚁停留在阴影部分的概率为( )
一只蚂蚁在如图所示的正方形地砖上爬行,蚂蚁停留在阴影部分的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
16.下列一元二次方程有两个相等实数根的是( )
| A. | x2-2x+1=0 | B. | 2x2-x+1=0 | C. | 4x2-2x-3=0 | D. | x2-6x=0 |
 如图,射线CF、AE与直线GH分别交于D、B,连接AD、CB,若∠HBE+∠GDC=180°,∠A=∠C,DA平分∠BDF.
如图,射线CF、AE与直线GH分别交于D、B,连接AD、CB,若∠HBE+∠GDC=180°,∠A=∠C,DA平分∠BDF.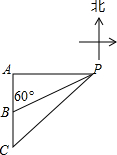 如图,已知一艘船以每小时20海里的速度向正南行驶,上午10时在A处见灯塔P在正东,1小时后行至B处,观察灯塔P的方向是北60°东,求正午12时船行驶至C处距灯塔P的距离.(答案可带根号)
如图,已知一艘船以每小时20海里的速度向正南行驶,上午10时在A处见灯塔P在正东,1小时后行至B处,观察灯塔P的方向是北60°东,求正午12时船行驶至C处距灯塔P的距离.(答案可带根号) 如图,边长为1的正方形ABCD,点M从点A出发以每秒1个单位长度的速度向点B运动,点N从点A出发以每秒3个单位长度的速度沿A→D→C→B的路径向点B运动,当一个点到达点B时,另一个点也随之停止运动,设△AMN的面积为s,运动时间为t秒,则能大致反映s与t的函数关系的图象是( )
如图,边长为1的正方形ABCD,点M从点A出发以每秒1个单位长度的速度向点B运动,点N从点A出发以每秒3个单位长度的速度沿A→D→C→B的路径向点B运动,当一个点到达点B时,另一个点也随之停止运动,设△AMN的面积为s,运动时间为t秒,则能大致反映s与t的函数关系的图象是( )


