题目内容
15. 如图,边长为1的正方形ABCD,点M从点A出发以每秒1个单位长度的速度向点B运动,点N从点A出发以每秒3个单位长度的速度沿A→D→C→B的路径向点B运动,当一个点到达点B时,另一个点也随之停止运动,设△AMN的面积为s,运动时间为t秒,则能大致反映s与t的函数关系的图象是( )
如图,边长为1的正方形ABCD,点M从点A出发以每秒1个单位长度的速度向点B运动,点N从点A出发以每秒3个单位长度的速度沿A→D→C→B的路径向点B运动,当一个点到达点B时,另一个点也随之停止运动,设△AMN的面积为s,运动时间为t秒,则能大致反映s与t的函数关系的图象是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据题意,分3种情况:(1)当点N在AD上运动时;(2)当点N在CD上运动时;(3)当点N在BC上运动时;求出△AMN的面积s关于t的解析式,进而判断出能大致反映s与t的函数关系的图象是哪个即可.
解答 解:(1)如图1,
当点N在AD上运动时,
s=$\frac{1}{2}$AM•AN=$\frac{1}{2}$×t×3t=$\frac{3}{2}$t2.
(2)如图2,
当点N在CD上运动时,
s=$\frac{1}{2}$AM•AD=t×1$\frac{1}{2}$=$\frac{1}{2}$t.
(3)如图3,
当点N在BC上运动时,
s=$\frac{1}{2}$AM•BN=$\frac{1}{2}$×t×(3-3t)=-$\frac{3}{2}$t2+$\frac{3}{2}$t
综上可得,能大致反映s与t的函数关系的图象是选项D中的图象.
故选:D.
点评 此题主要考查了动点问题的函数图象,要熟练掌握,解答此题的关键是要明确:函数图象是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.用图象解决问题时,要理清图象的含义即会识图.

练习册系列答案
相关题目
10. 一个几何体的三视图如图所示,那么这个几何体是( )
一个几何体的三视图如图所示,那么这个几何体是( )
 一个几何体的三视图如图所示,那么这个几何体是( )
一个几何体的三视图如图所示,那么这个几何体是( )| A. | 圆锥 | B. | 圆柱 | C. | 长方体 | D. | 三棱柱 |
7.$\frac{1}{9}$的平方根是( )
| A. | $\frac{1}{3}$ | B. | $±\frac{1}{3}$ | C. | $-\frac{1}{3}$ | D. | $±\frac{1}{81}$ |
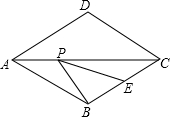 如图,菱形ABCD的边长为2,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为$\sqrt{3}$+1.
如图,菱形ABCD的边长为2,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为$\sqrt{3}$+1.