题目内容
18.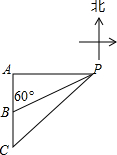 如图,已知一艘船以每小时20海里的速度向正南行驶,上午10时在A处见灯塔P在正东,1小时后行至B处,观察灯塔P的方向是北60°东,求正午12时船行驶至C处距灯塔P的距离.(答案可带根号)
如图,已知一艘船以每小时20海里的速度向正南行驶,上午10时在A处见灯塔P在正东,1小时后行至B处,观察灯塔P的方向是北60°东,求正午12时船行驶至C处距灯塔P的距离.(答案可带根号)
分析 在直角△ABP中利用三角函数求得AP的长,然后在直角△ACP中,利用勾股定理求解.
解答 解:∵在直角△ABP中,tan∠ABP=$\frac{AP}{AB}$,
∴AP=AB•tan∠ABP=20$\sqrt{3}$(海里).
又∵直角△ACP中,AC=2×20=40(海里),
∴PC=$\sqrt{A{C}^{2}+A{P}^{2}}$=$\sqrt{4{0}^{2}+(20\sqrt{3})^{2}}$=20$\sqrt{7}$(海里).
答:正午12时船行驶至C处距灯塔P的距离是20$\sqrt{7}$海里.
点评 本题主要考查了方向角含义,正确记忆三角函数的定义是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.对于一次函数y=-2x+4,下列结论错误的是( )
| A. | 若两点A(x1,y1),B(x2,y2)在该函数图象上,且x1<x2,则y1>y2 | |
| B. | 函数的图象不经过第三象限 | |
| C. | 函数的图象向下平移4个单位长度得y=-2x的图象 | |
| D. | 函数的图象与x轴的交点坐标是(0,4) |
10. 一个几何体的三视图如图所示,那么这个几何体是( )
一个几何体的三视图如图所示,那么这个几何体是( )
 一个几何体的三视图如图所示,那么这个几何体是( )
一个几何体的三视图如图所示,那么这个几何体是( )| A. | 圆锥 | B. | 圆柱 | C. | 长方体 | D. | 三棱柱 |
7.$\frac{1}{9}$的平方根是( )
| A. | $\frac{1}{3}$ | B. | $±\frac{1}{3}$ | C. | $-\frac{1}{3}$ | D. | $±\frac{1}{81}$ |
 如图,△ABC≌△BAD,A、C的对应点分别是B、D.若AB=9,BC=12,AC=7,则BD=7.
如图,△ABC≌△BAD,A、C的对应点分别是B、D.若AB=9,BC=12,AC=7,则BD=7.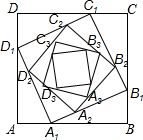 如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1、C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2=B1B2=C1C2=D1D2=$\frac{1}{3}$A1B2,….依次规律继续下去,则正方形AnBnCnDn的面积为$\frac{{5}^{n}}{{9}^{n}}{a}^{2}$.
如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1、C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2=B1B2=C1C2=D1D2=$\frac{1}{3}$A1B2,….依次规律继续下去,则正方形AnBnCnDn的面积为$\frac{{5}^{n}}{{9}^{n}}{a}^{2}$.