题目内容
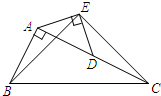 如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连结BE、EC.试判断△BCE的形状,并证明你的结论.
如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连结BE、EC.试判断△BCE的形状,并证明你的结论.考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:根据题意易证AB=CD,AE=DE,∠EAB=∠EDC,即可证明△EAB≌△EDC,可得∠AEB=∠DEC,EB=EC,根据∠AEB+∠BED=90°即可解题.
解答:解:△BCE 是等腰直角三角形.
∵AC=2AB,点D是AC的中点,
∴AB=AD=CD,
∵∠EAD=∠EDA=45°,
∴∠EAB=∠EDC=135°,
在△EAB和△EDC中,
∵
,
∴△EAB≌△EDC(SAS),
∴∠AEB=∠DEC,EB=EC,
∴∠BEC=∠AED=90°,
∴BE=EC,BE⊥EC,
∴△BCE是等腰直角三角形.
∵AC=2AB,点D是AC的中点,
∴AB=AD=CD,
∵∠EAD=∠EDA=45°,
∴∠EAB=∠EDC=135°,
在△EAB和△EDC中,
∵
|
∴△EAB≌△EDC(SAS),
∴∠AEB=∠DEC,EB=EC,
∴∠BEC=∠AED=90°,
∴BE=EC,BE⊥EC,
∴△BCE是等腰直角三角形.
点评:本题主要考查了全等三角形的判定与性质,本题中求证△EAB≌△EDC是解题的关键,证明线段相等的问题一般的解决方法是转化为证明三角形全等.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
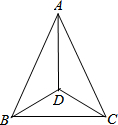 如图,已知在△ABC中,AB=AC,点D是△ABC内一点,且∠ABD=∠ACD,求证:AD是∠BAC的平分线.
如图,已知在△ABC中,AB=AC,点D是△ABC内一点,且∠ABD=∠ACD,求证:AD是∠BAC的平分线.
 数):
数): 如图所示是淮河的一段,两岸AB∥CD,河岸AB上有一排大树.小明为了测量该段河的宽度,先用测角仪在河岸CD的M处测得∠α=33°,然后沿河岸走40米到达N点,测得∠β=64°.请你帮小明算出河宽ER(结果保留整数).
如图所示是淮河的一段,两岸AB∥CD,河岸AB上有一排大树.小明为了测量该段河的宽度,先用测角仪在河岸CD的M处测得∠α=33°,然后沿河岸走40米到达N点,测得∠β=64°.请你帮小明算出河宽ER(结果保留整数).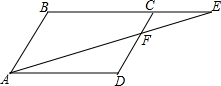 如图,四边形ABCD为?,BC=2CE,则S△CEF:S四边形ABCD=
如图,四边形ABCD为?,BC=2CE,则S△CEF:S四边形ABCD=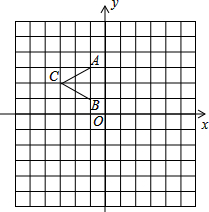 如图,△ABC三个顶点坐标分别为A(-1,3),B(-1,1),C(-3,2)
如图,△ABC三个顶点坐标分别为A(-1,3),B(-1,1),C(-3,2) 如图,AB是⊙O的直径,弦CD⊥AB,交AB于点E,∠CDB=30°,⊙O的半径为2cm,求弦CD的长.
如图,AB是⊙O的直径,弦CD⊥AB,交AB于点E,∠CDB=30°,⊙O的半径为2cm,求弦CD的长.