题目内容
13.不等式-2x<4的解集是( )| A. | x>2 | B. | x<2 | C. | x<-2 | D. | x>-2 |
分析 两边同时除以-2,把x的系数化成1即可求解.
解答 解:两边同时除以-2,得:x>-2.
故选D.
点评 本题考查了解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错.
解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
3. 如图,方格纸中是9个完全相同的正方形,则∠1+∠2=( )
如图,方格纸中是9个完全相同的正方形,则∠1+∠2=( )
 如图,方格纸中是9个完全相同的正方形,则∠1+∠2=( )
如图,方格纸中是9个完全相同的正方形,则∠1+∠2=( )| A. | 75° | B. | 80° | C. | 90° | D. | 105° |
18.如果2x3myn+4与-3x9y3n是同类项,那么m、n的值分别为( )
| A. | m=-2,n=3 | B. | m=2,n=3 | C. | m=3,n=2 | D. | m=3,n=2 |
3.若( )÷$\frac{2}{3}$xn=$\frac{1}{2}$xn-2xm+1,则括号内应填的代数式为( )
| A. | $\frac{1}{3}$x${\;}^{{n}^{2}}$-2xnm+1 | B. | $\frac{1}{3}$x${\;}^{{n}^{2}}$-$\frac{1}{3}$xnm+$\frac{2}{3}$xn | ||
| C. | $\frac{1}{3}$x2n-$\frac{4}{3}$xm+n+$\frac{2}{3}$xn | D. | $\frac{1}{3}$x2n-$\frac{4}{3}$xm+n+1 |
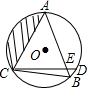 如图,在⊙O中,$\widehat{AD}$=$\widehat{AC}$,弦CD与弦AB交于点E,连接BC,若⊙O的半径长为4cm,∠ACD=60°,求图中阴影部分的面积.
如图,在⊙O中,$\widehat{AD}$=$\widehat{AC}$,弦CD与弦AB交于点E,连接BC,若⊙O的半径长为4cm,∠ACD=60°,求图中阴影部分的面积. 如图,∠1=70°,∠2=130°,直线m平移后得到直线n,则∠3=20°.
如图,∠1=70°,∠2=130°,直线m平移后得到直线n,则∠3=20°.