题目内容
3.若( )÷$\frac{2}{3}$xn=$\frac{1}{2}$xn-2xm+1,则括号内应填的代数式为( )| A. | $\frac{1}{3}$x${\;}^{{n}^{2}}$-2xnm+1 | B. | $\frac{1}{3}$x${\;}^{{n}^{2}}$-$\frac{1}{3}$xnm+$\frac{2}{3}$xn | ||
| C. | $\frac{1}{3}$x2n-$\frac{4}{3}$xm+n+$\frac{2}{3}$xn | D. | $\frac{1}{3}$x2n-$\frac{4}{3}$xm+n+1 |
分析 直接利用整式乘法运算法则求出答案.
解答 解:∵( )÷$\frac{2}{3}$xn=$\frac{1}{2}$xn-2xm+1,
∴($\frac{1}{2}$xn-2xm+1)×$\frac{2}{3}$xn=$\frac{1}{3}$x2n-$\frac{4}{3}$xm+n+$\frac{2}{3}$xn,
故括号内应填的代数式为:$\frac{1}{3}$x2n-$\frac{4}{3}$xm+n+$\frac{2}{3}$xn.
故选:C.
点评 此题主要考查了整式的除法运算,正确掌握运算法则是解题关键.

练习册系列答案
相关题目
13.不等式-2x<4的解集是( )
| A. | x>2 | B. | x<2 | C. | x<-2 | D. | x>-2 |
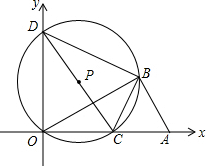 如图,在平面直角坐标系中,Rt△ABO的斜边OA在x轴上,点B在第一象限内,AO=4,∠BOA=30°.点C(t,0)是x轴正半轴上一动点(不与O,A重合),△OBC的外接圆⊙P与y轴的另一交点为D.
如图,在平面直角坐标系中,Rt△ABO的斜边OA在x轴上,点B在第一象限内,AO=4,∠BOA=30°.点C(t,0)是x轴正半轴上一动点(不与O,A重合),△OBC的外接圆⊙P与y轴的另一交点为D.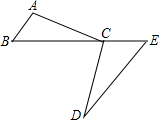 已知:如图,C为BE上一点,点A,D分别在BE两侧.AB∥ED,AB=CE,BC=ED.求证:∠A=∠DCE.
已知:如图,C为BE上一点,点A,D分别在BE两侧.AB∥ED,AB=CE,BC=ED.求证:∠A=∠DCE.