题目内容
18．
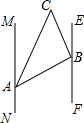如图，A，B两个村庄分别在两条公路MN和EF的边上，且MN∥EF，某施工队在A，B，C三个村之间修了三条笔直的路．若∠MAB=65°，∠CBE=25°，AB=160km，BC=120km，则A，C两村之间的距离为（ ）| A． | 250km | B． | 240km | C． | 200km | D． | 180km |
分析 直接利用平行线的性质得出∠ABC的度数，再利用勾股定理得出答案．
解答 解：∵MN∥EF，∠MAB=65°，
∴∠ABF=65°，
∵∠CBE=25°，
∴∠ABC=180°-65°-25°=90°，
∴△ABC是直角三角形，
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=200（km）．
故选：C．
点评 此题主要考查了勾股定理以及勾股定理的逆定理等知识，正确得出△ABC是直角三角形是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．借助表格进行多项式乘多项式运算，可以方便合并同类项得出结果．下面尝试利用表格试一试．
例题：（a+b）（a-b）
解填表
则（a+b）（a-b）=a2-b2．
根据所学完成下列问题．
（1）如表，填表计算（x+2）（x2-2x+4），（m+3）（m2-3m+9），直接写出结果．
结果为x3+8； 结果为m3+27．
（2）根据以上获得的经验填表：
结果为△3+○3，根据以上探索，请用字母a、b来表示发现的公式为（a+b）（a2-ab+b2）=a3+b3．
（3）用公式计算：（2x+3y）（4x2-6xy+9y2）=8x3+27y3；
因式分解：27m3-8n3=（3m-2n）（9m2+6mn+4n2）．
例题：（a+b）（a-b）
解填表
 | a | b |
| a | a2 | ab |
| -b | -ab | -b2 |
根据所学完成下列问题．
（1）如表，填表计算（x+2）（x2-2x+4），（m+3）（m2-3m+9），直接写出结果．
 | x2 | -2x | 4 |
| x | x3 | -2x2 | 4x |
| +2 | 2x2 | -4x | 8 |
 | m2 | -3m | 9 |
| m | m3 | -3m2 | 9m |
| +3 | 3m2 | -9m | 27 |
（2）根据以上获得的经验填表：
 | |||
| △ | △3 | ||
| ○ | ○3 |
（3）用公式计算：（2x+3y）（4x2-6xy+9y2）=8x3+27y3；
因式分解：27m3-8n3=（3m-2n）（9m2+6mn+4n2）．
已知等边三角形ABC，AB=12，以AB为直径的半圆与BC边交于点D，过点D作DF⊥AC，垂足为F，过点F作FG⊥AB，垂足为G，连接GD，
甲、乙两车分别从A，B两地同时相向匀速行驶．当乙车到达A地后，继续保持原速向远离B的方向行驶，而甲车到达B地后立即掉头，并保持原速与乙车同向行驶，经过一段时间后两车同时到达C地．设两车行驶的时间为x（小时），两车之间的距离为y（千米），y与x之间的函数关系如图所示，则B，C两地相距600千米．