题目内容
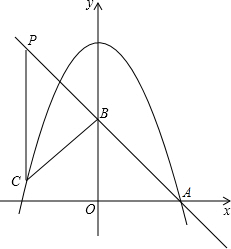 二次函数y=ax2+4的图象与x轴正半轴交于点A(2,0),点B(0,2)在y轴上,点P是直线AB上的一个动点,过点P作PC∥y轴交抛物线于点C,设点P的横坐标为m(m<2),求当△PBC是直角三角形时,直接写出m的值.
二次函数y=ax2+4的图象与x轴正半轴交于点A(2,0),点B(0,2)在y轴上,点P是直线AB上的一个动点,过点P作PC∥y轴交抛物线于点C,设点P的横坐标为m(m<2),求当△PBC是直角三角形时,直接写出m的值.考点:二次函数综合题
专题:
分析:把点(2,0)代入二次函数y=ax2+4,根据待定系数法可求二次函数解析式,设直线AB的解析式为y=kx+b,根据待定系数法可求直线AB的解析式,再分∠PBC=90°,∠PCB=90°两种情况讨论即可求解.
解答:解:把点(2,0)代入二次函数y=ax2+4,可得
4a+4=0,
解得a=-1,
则二次函数解析式为y=-x2+4,
设直线AB的解析式为y=kx+b,
把点(2,0),(0,2)代入可得
,
解得
则直线AB的解析式为y=-x+2,
①设抛物线与x负半轴交于点D,易得△ABD为等腰直角三角形,其中∠ABD为直角.
即过点B、D的直线是垂直于直线AP,
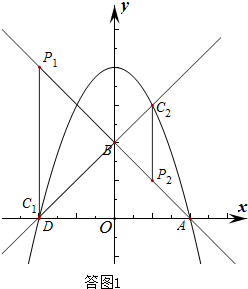
当∠PBC=90°时,即点C在直线BD上,如答图1,
设直线BD的解析式为y=k′x+b′,
把点B(0,2),点D(-2,0)代入,可得直线BD的解析式为y=x+2,
联立二次函数解析式可得
,
解得
,
.
则m的值为-2或1;
②当∠PCB=90°时,
∵PC∥y轴,
∴CB⊥y轴
过点B作直线l垂直于y轴,如答图2,
C点的纵坐标为2,将其代入抛物线解析式中,
当y=2时,-x2+4=2,解得x=±
,
则m的值为-
或
.
综上所述,m的值为-2或1或-
或
.
4a+4=0,
解得a=-1,
则二次函数解析式为y=-x2+4,
设直线AB的解析式为y=kx+b,
把点(2,0),(0,2)代入可得
|
解得
|

则直线AB的解析式为y=-x+2,
①设抛物线与x负半轴交于点D,易得△ABD为等腰直角三角形,其中∠ABD为直角.
即过点B、D的直线是垂直于直线AP,
当∠PBC=90°时,即点C在直线BD上,如答图1,
设直线BD的解析式为y=k′x+b′,
把点B(0,2),点D(-2,0)代入,可得直线BD的解析式为y=x+2,
联立二次函数解析式可得
|
解得
|
|

则m的值为-2或1;
②当∠PCB=90°时,
∵PC∥y轴,
∴CB⊥y轴
过点B作直线l垂直于y轴,如答图2,
C点的纵坐标为2,将其代入抛物线解析式中,
当y=2时,-x2+4=2,解得x=±
| 2 |
则m的值为-
| 2 |
| 2 |
综上所述,m的值为-2或1或-
| 2 |
| 2 |
点评:考查了二次函数综合题,涉及的知识点有:待定系数法求二次函数解析式,待定系数法求直线的解析式,直角三角形的性质,方程思想,以及分类思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 李师傅驾车到外地送货,出发前汽车油箱有50升油,行驶若干小时后,在加油站加油若干升后继续行驶.如图是表示汽车油箱中剩余油量y(单位:升)与行驶时间t(单位:时)之间函数关系的图象.请根据图象解答下列问题:
李师傅驾车到外地送货,出发前汽车油箱有50升油,行驶若干小时后,在加油站加油若干升后继续行驶.如图是表示汽车油箱中剩余油量y(单位:升)与行驶时间t(单位:时)之间函数关系的图象.请根据图象解答下列问题: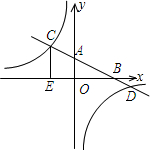 已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=
已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=