题目内容
 如图,一轮船由西向东航行,从A点到B点航程为12千米,分别在A、B两处望小岛P,测得∠BAP=15°,∠DBP=30°.若小岛P周围6.8千米内有暗礁,问该船一直向东航行有无触礁的危险?
如图,一轮船由西向东航行,从A点到B点航程为12千米,分别在A、B两处望小岛P,测得∠BAP=15°,∠DBP=30°.若小岛P周围6.8千米内有暗礁,问该船一直向东航行有无触礁的危险?考点:解直角三角形的应用-仰角俯角问题
专题:
分析:过P作PD垂直与AB,交AB延长线于点D,如图所示,根据∠A=15°,∠PBD=30°,可得AB=PB,PB=2PD=12,求出x的值,然后和6.8进行比较,判断是否有触礁的危险.
解答:解:有危险,理由如下:
过点P作PD⊥AB,交AB的延长线于点D,如图所示:
∵由题意可知:∠A=15°,∠PBD=30°,
∴∠BPA=∠PBD-∠A=15°,即∠BPA=∠A,
∴PB=AB=12(千米),
在Rt△BPD中,∠PBD=30°,PB=12千米,
∴PD=
PB=6<6.8,
∴轮船不改变方向仍继续向前航行有触礁的危险.

过点P作PD⊥AB,交AB的延长线于点D,如图所示:
∵由题意可知:∠A=15°,∠PBD=30°,
∴∠BPA=∠PBD-∠A=15°,即∠BPA=∠A,
∴PB=AB=12(千米),
在Rt△BPD中,∠PBD=30°,PB=12千米,
∴PD=
| 1 |
| 2 |
∴轮船不改变方向仍继续向前航行有触礁的危险.
点评:本题考查了解直角三角形的应用,涉及了等腰三角形的判定与性质,三角形的外角性质,以及含30°直角三角形的性质,解答本题的关键是根据仰角和俯角构造直角三角形,利用三角函数的知识求解,难度一般.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
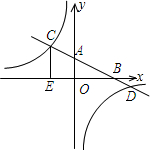 已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=
已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO= 如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.
如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.