题目内容
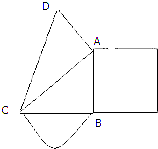 如图,Rt△ABC中,以AB为边向外作正方形,以BC为直径向外作半圆,且正方形面积与半圆面积之比为9:2π,现已AC为直角边向外作Rt△ACD,若AD=8,CD=17,则正方形的面积为
如图,Rt△ABC中,以AB为边向外作正方形,以BC为直径向外作半圆,且正方形面积与半圆面积之比为9:2π,现已AC为直角边向外作Rt△ACD,若AD=8,CD=17,则正方形的面积为考点:正多边形和圆
专题:
分析:先根据勾股定理求出AC2的值,再由三角形ABC是直角三角形得出AB2+BC2=AC2,S正方形=AB2,S半圆=
=
,再由正方形面积与半圆面积之比为9:2π即可得出结论.
(
| ||
| 2 |
| BC2π |
| 8 |
解答:解:∵△ACD是直角三角形,AD=8,CD=17,
∴AC2=CD2-AD2=172-82=225.
∵S正方形=AB2,S半圆=
=
,正方形面积与半圆面积之比为9:2π,
∴
=
①,
∵AB2+BC2=AC2②,
①②联立得,AB2=81,即正方形的面积为81.
∴AC2=CD2-AD2=172-82=225.
∵S正方形=AB2,S半圆=
(
| ||
| 2 |
| BC2π |
| 8 |
∴
| AB2 | ||
|
| 9 |
| 2π |
∵AB2+BC2=AC2②,
①②联立得,AB2=81,即正方形的面积为81.
点评:本题考查的是正多边形和圆,熟知勾股定理、正方形的性质及圆的面积公式是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将多项式 3x3-2x2+4x-5添括号后正确的是( )
| A、3x3-(2 x2+4x-5 ) |
| B、( 3x3+4x)-(2 x2+5) |
| C、(3x3-5)+(-2 x2-4x) |
| D、2 x2+(3x3+4x-5) |
 画一个三角形,使A′B′=AB,B′C′=BC,C′A′=CA.(保留作图痕迹)
画一个三角形,使A′B′=AB,B′C′=BC,C′A′=CA.(保留作图痕迹)
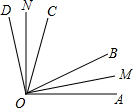 如图所示,OB、OC是∠AOD内的任意两条射线,OM平分∠AOB,ON平分∠COD.若∠AOD=120°,∠BOC=70°.求∠MON使多少度?
如图所示,OB、OC是∠AOD内的任意两条射线,OM平分∠AOB,ON平分∠COD.若∠AOD=120°,∠BOC=70°.求∠MON使多少度?