题目内容
2.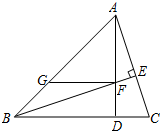 如图,已知:△ABC的高AD与高BE相交于点F,且∠ABC=45°,过点F作FG∥BC交AB于点G,求证:FG+CD=BD.
如图,已知:△ABC的高AD与高BE相交于点F,且∠ABC=45°,过点F作FG∥BC交AB于点G,求证:FG+CD=BD.小方同学在解答此题时,利用了上述结论,她的方法如下:
连接CF并延长,交AB于点M,
∵△ABC的高AD与高BE相交于点F,
∴CM为△ABC的高.
(请你写出小方没完成的证明过程.)
分析 首先根据等腰直角三角形的性质得出AD=BD,再在Rt△BCM中,∠MBC=45°,进而得出CD=DF,AF=FG,即可得出答案.
解答 证明:如图,连接CF并延长,交AB于点M,
在Rt△ADB中,AD=BD,
∵在Rt△BCM中,∠MBC=45°,
∴∠BCM=45°,即∠DCF=45°,
∴在Rt△CFD中,CD=DF,
∵FG∥BC,
∴∠AGF=∠ABC=45°,
∴在Rt△AFG中,AF=FG,
∴FG+CD=AF+DF=AD=BD.
点评 此题主要考查了等腰直角三角形的性质的知识,根据Rt△ADB得出AD=BD是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下面的图案是由一个图形经过多次轴对称变换得到的,在这些对称轴中,共有平行线( )

| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
 如图,一次函数y=$\frac{\sqrt{3}}{3}$x+b的图象与x轴相交于点A(5$\sqrt{3}$,0),与y轴相交于点B
如图,一次函数y=$\frac{\sqrt{3}}{3}$x+b的图象与x轴相交于点A(5$\sqrt{3}$,0),与y轴相交于点B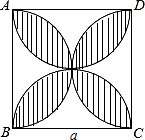 如图,正方形的边长为a,以各边为直径在正方形内画半圆.
如图,正方形的边长为a,以各边为直径在正方形内画半圆. 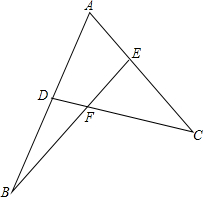 如图:∠ADC+∠AEB=180°,AB=k•AC,判断BE与CD的关系,并加以证明.
如图:∠ADC+∠AEB=180°,AB=k•AC,判断BE与CD的关系,并加以证明.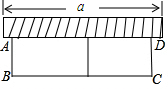 如图,有一个长为24米的篱笆,一面利用墙(墙的最大长度a为15米)围成的中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.
如图,有一个长为24米的篱笆,一面利用墙(墙的最大长度a为15米)围成的中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.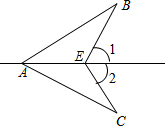 如图,∠1=∠2,要使△ABE≌△ACE,若以“SAS”为依据,还缺条件BE=CE.
如图,∠1=∠2,要使△ABE≌△ACE,若以“SAS”为依据,还缺条件BE=CE.