题目内容
11.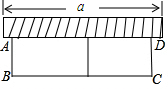 如图,有一个长为24米的篱笆,一面利用墙(墙的最大长度a为15米)围成的中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.
如图,有一个长为24米的篱笆,一面利用墙(墙的最大长度a为15米)围成的中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.(1)求S与x的函数关系式;
(2)如果要围成花圃的面积为36平方米,求AB的长为多少米?
(3)如果要使围成花圃面积最大,求AB的长为多少米?
分析 (1)可先用篱笆的长表示出BC的长,然后根据矩形的面积=长×宽,得出S与x的函数关系式;
(2)根据(1)的函数关系式,将S=36代入其中,求出x的值即可;
(3)根据二次函数的性质求出自变量取值范围内的最值.
解答 解:(1)花圃的宽AB为x米,则BC=(24-3x)米,
∴S=x(24-3x),
即S=-3x2+24x(3≤x<8);
(2)当S=36时,-3x2+24x=36,
解得x1=2,x2=6,
当x=2时,24-3x=18>15,不合题意,舍去;
当x=6时,24-3x=6<15,符合题意,
故AB的长为6米.
(3)S=-3x2+24x=-3(x-4)2+48,
∵3≤x<8,
∴当x=4米时面积最大,最大面积为48平方米.
点评 本题考查了二次函数的综合应用,根据已知条件列出二次函数式是解题的关键.要注意题中自变量的取值范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.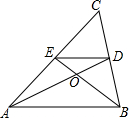 如图,在△ABC中,AD、BE是两条中线,则S△DOB:S△AOB=( )
如图,在△ABC中,AD、BE是两条中线,则S△DOB:S△AOB=( )
 如图,在△ABC中,AD、BE是两条中线,则S△DOB:S△AOB=( )
如图,在△ABC中,AD、BE是两条中线,则S△DOB:S△AOB=( )| A. | 1:2 | B. | 2:3 | C. | 1:3 | D. | 1:4 |
1.如果□+2=0,那么“□”内填的数的是( )
| A. | 2 | B. | -2 | C. | 0 | D. | -1 |
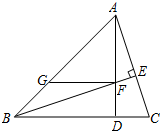 如图,已知:△ABC的高AD与高BE相交于点F,且∠ABC=45°,过点F作FG∥BC交AB于点G,求证:FG+CD=BD.
如图,已知:△ABC的高AD与高BE相交于点F,且∠ABC=45°,过点F作FG∥BC交AB于点G,求证:FG+CD=BD.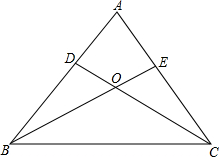 如图,BE与CD相交于点O,已知AD=AE,∠ADC=∠AEB.
如图,BE与CD相交于点O,已知AD=AE,∠ADC=∠AEB.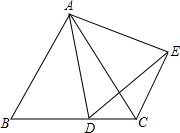 已知△ABC为等边三角形,D为BC边上一点,△ADE也是等边三角形
已知△ABC为等边三角形,D为BC边上一点,△ADE也是等边三角形 如图,AB是⊙O的弦,AB=4,点C是⊙O上的一个动点,且∠ACB=45°.若点M,N分别是AB,BC的中点,则MN长的最大值是2$\sqrt{2}$.
如图,AB是⊙O的弦,AB=4,点C是⊙O上的一个动点,且∠ACB=45°.若点M,N分别是AB,BC的中点,则MN长的最大值是2$\sqrt{2}$.