题目内容
10.已知:y=x2-(2m+1)x+m2+m(m>0),设函数与x轴的两个交点分别为(x1,0)、(x2,0)(其中x1<x2).且a=x1-4x2,问当m取何值时,a≤4?分析 将函数解析式转化为两点式方程,即可得到函数与x轴的两个交点,然后在m>0的情况下解不等式x1-4x2≤4即可.
解答 解:∵y=x2-(2m+1)x+m2+m=(x-m)(x-m-1),
∴x1=m,x2=m+1,
∴a=x1-4x2=m-4m-4=-3m-4.
则$\left\{\begin{array}{l}{m>0}\\{-3m-4≤4}\end{array}\right.$,
解得m>0,
所以当m>0时,a≤4.
点评 本题考查了抛物线与x轴的交点.解题时,需要掌握二次函数解析式的三种形式间的转换.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
1.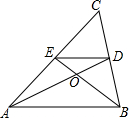 如图,在△ABC中,AD、BE是两条中线,则S△DOB:S△AOB=( )
如图,在△ABC中,AD、BE是两条中线,则S△DOB:S△AOB=( )
 如图,在△ABC中,AD、BE是两条中线,则S△DOB:S△AOB=( )
如图,在△ABC中,AD、BE是两条中线,则S△DOB:S△AOB=( )| A. | 1:2 | B. | 2:3 | C. | 1:3 | D. | 1:4 |
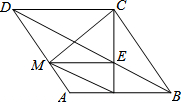 己知:如图,在菱形ABCD中,点M、N分别在边AD、AB,∠DCM=∠BCN,CN与BD交于点E.
己知:如图,在菱形ABCD中,点M、N分别在边AD、AB,∠DCM=∠BCN,CN与BD交于点E.
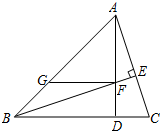 如图,已知:△ABC的高AD与高BE相交于点F,且∠ABC=45°,过点F作FG∥BC交AB于点G,求证:FG+CD=BD.
如图,已知:△ABC的高AD与高BE相交于点F,且∠ABC=45°,过点F作FG∥BC交AB于点G,求证:FG+CD=BD. 如图,BE与CD相交于点O,已知AD=AE,∠ADC=∠AEB.
如图,BE与CD相交于点O,已知AD=AE,∠ADC=∠AEB. 如图,AB是⊙O的弦,AB=4,点C是⊙O上的一个动点,且∠ACB=45°.若点M,N分别是AB,BC的中点,则MN长的最大值是2$\sqrt{2}$.
如图,AB是⊙O的弦,AB=4,点C是⊙O上的一个动点,且∠ACB=45°.若点M,N分别是AB,BC的中点,则MN长的最大值是2$\sqrt{2}$.