题目内容
在△ABC中,∠BAC=90°,AB=AC,P为△ABC内一点,且BP=AB,∠ABP=30°,求证:PA=PC.
考点:全等三角形的判定与性质,等边三角形的性质,等腰直角三角形
专题:
分析:延长BP交AC于E,延长AP交BC于D,连接DE,根据△ACD∽△BCE可得△CDE为等腰直角三角形,即ED=DC,根据角的关系即可求得PD=ED,即可解题.
解答:解:延长BP交AC于E,延长AP交BC于D,连接DE,

∵∠BAC=90°,AB=AC,BP=AB,∠ABP=30°
∴∠BAP=∠BPA=75°,∠CAD=∠CBE=15°,
∴△ACD∽△BCE,
∴
=
=
,
∵∠ACB=45°,
∴△CDE为等腰直角三角形,∴ED=DC,且ED⊥BC,
∴∠PED=90°-∠DBE=90°-15°=75°,
∴∠PED=∠EPD=75°,
∴DP=DE,∴DP=DC,
∵∠BDP=180°-∠DBP-∠BPD=60°,
∴∠DPC=∠DCP=30°,
∴∠PCA=15°,
∴AP=PC.

∵∠BAC=90°,AB=AC,BP=AB,∠ABP=30°
∴∠BAP=∠BPA=75°,∠CAD=∠CBE=15°,
∴△ACD∽△BCE,
∴
| CE |
| CD |
| BC |
| AC |
| 2 |
∵∠ACB=45°,
∴△CDE为等腰直角三角形,∴ED=DC,且ED⊥BC,
∴∠PED=90°-∠DBE=90°-15°=75°,
∴∠PED=∠EPD=75°,
∴DP=DE,∴DP=DC,
∵∠BDP=180°-∠DBP-∠BPD=60°,
∴∠DPC=∠DCP=30°,
∴∠PCA=15°,
∴AP=PC.
点评:本题考查了等腰三角形腰长相等的性质,考查了等腰三角形的判定,本题中求证DP=CD是解题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
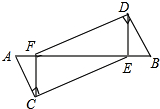 如图,已知A,F,E,B四点共线,AC⊥CE,BD⊥DF,AE=BF,AC=BD.
如图,已知A,F,E,B四点共线,AC⊥CE,BD⊥DF,AE=BF,AC=BD.